Question Number 93847 by i jagooll last updated on 15/May/20
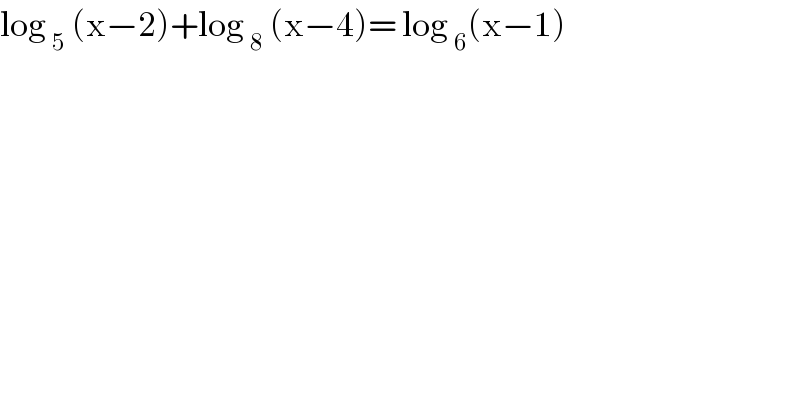
$$\mathrm{log}\:_{\mathrm{5}} \:\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{log}\:_{\mathrm{8}} \:\left(\mathrm{x}−\mathrm{4}\right)=\:\mathrm{log}\:_{\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right) \\ $$
Commented by john santu last updated on 15/May/20
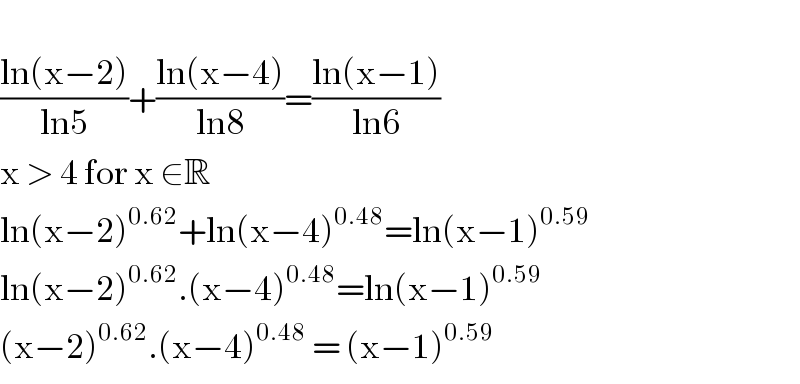
$$ \\ $$$$\frac{\mathrm{ln}\left(\mathrm{x}−\mathrm{2}\right)}{\mathrm{ln5}}+\frac{\mathrm{ln}\left(\mathrm{x}−\mathrm{4}\right)}{\mathrm{ln8}}=\frac{\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{ln6}}\: \\ $$$$\mathrm{x}\:>\:\mathrm{4}\:\mathrm{for}\:\mathrm{x}\:\in\mathbb{R} \\ $$$$\mathrm{ln}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{0}.\mathrm{62}} +\mathrm{ln}\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{0}.\mathrm{48}} =\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{0}.\mathrm{59}} \\ $$$$\mathrm{ln}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{0}.\mathrm{62}} .\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{0}.\mathrm{48}} =\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{0}.\mathrm{59}} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{0}.\mathrm{62}} .\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{0}.\mathrm{48}} \:=\:\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{0}.\mathrm{59}} \\ $$
Commented by i jagooll last updated on 15/May/20
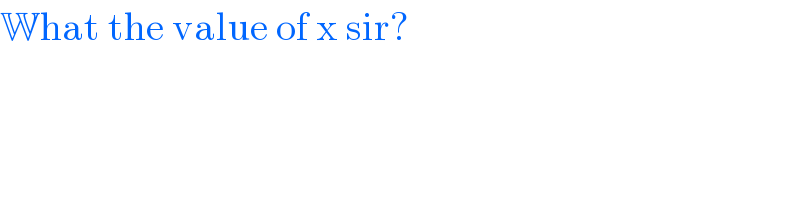
$$\mathbb{W}\mathrm{hat}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{sir}? \\ $$
