log-x-x-2-1-1-

Question Number 146272 by mathdanisur last updated on 12/Jul/21

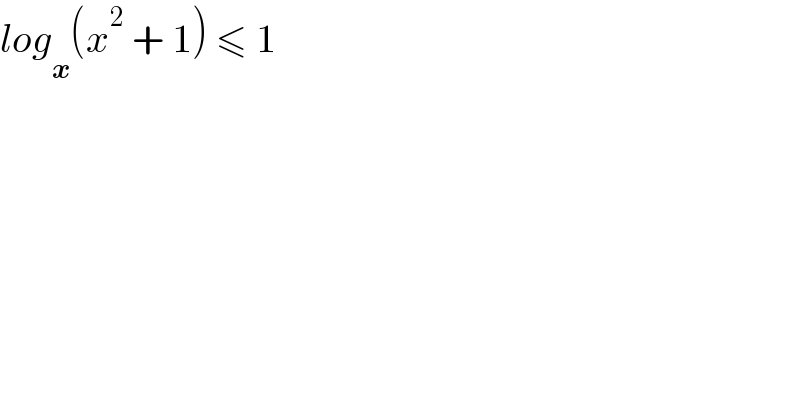
{l o g}_{x} (x^{2} + 1) ⩽ 1

Commented by iloveisrael last updated on 13/Jul/21

\log_{x} (x^{2} + 1) ⩽ \log_{x} (x)

\Rightarrow (x - 1) (x^{2} - x + 1) ⩽ 0

since for x^{2} - x + 1 > 0 \forall x \in R

then x < 1, x \neq 1 \cap x > 0

solution is 0 < x < 1

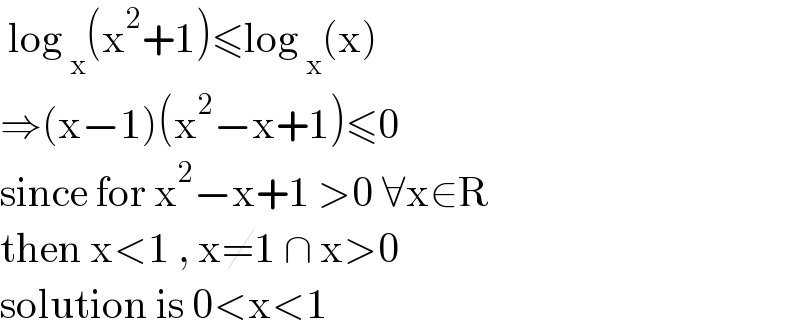
Commented by mathdanisur last updated on 13/Jul/21

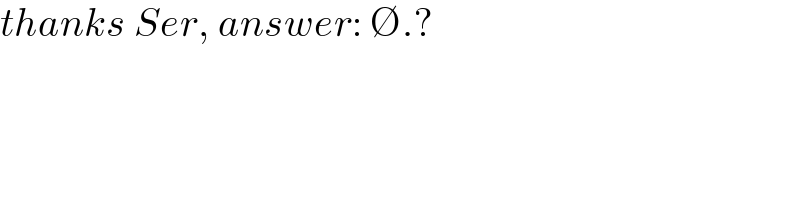
t h a n k s S e r, a n s w e r : \emptyset . ?

Commented by iloveisrael last updated on 13/Jul/21

no

Answered by gsk2684 last updated on 12/Jul/21

x^{2} + 1 ⩽ x^{1} i f x > 1

x^{2} - x + 1 ⩽ 0

{(x - \frac{1}{2})}^{2} - \frac{1}{4} + 1 ⩽ 0

{(x - \frac{1}{2})}^{2} + \frac{3}{4} ⩽ 0 n o s o l u t i o n

a n d

x^{2} + 1 ⩾ x i f 0 < x < 1

x^{2} - x + 1 ⩾ 0

{(x - \frac{1}{2})}^{2} + \frac{3}{4} ⩾ 0

t r u e f o r a l l x

s o l u t i o n s e t i s (0 1)

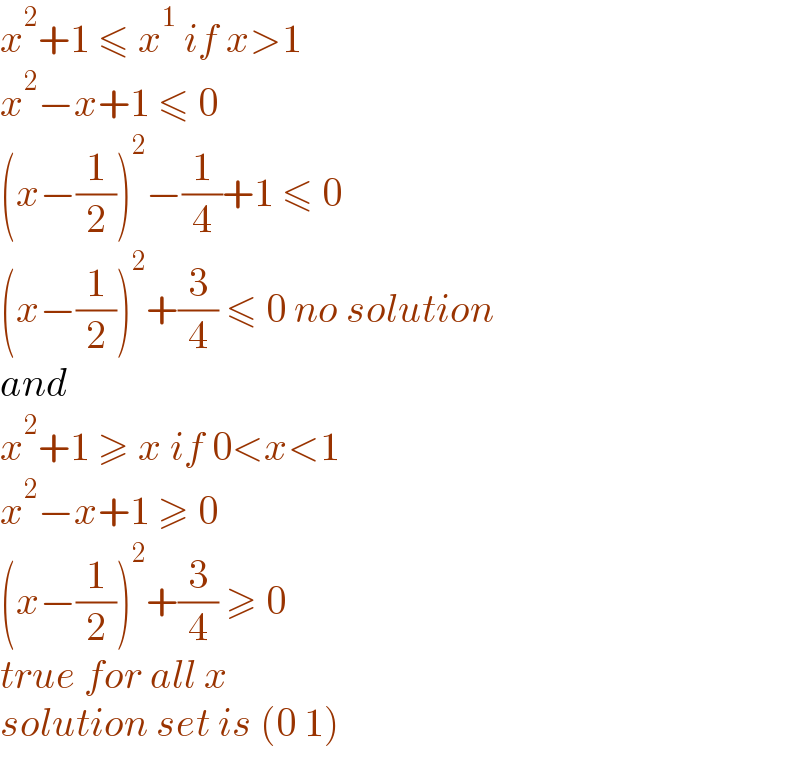
Commented by mathdanisur last updated on 12/Jul/21

c o o l t h a n k s S e r