Question Number 148573 by mathdanisur last updated on 29/Jul/21
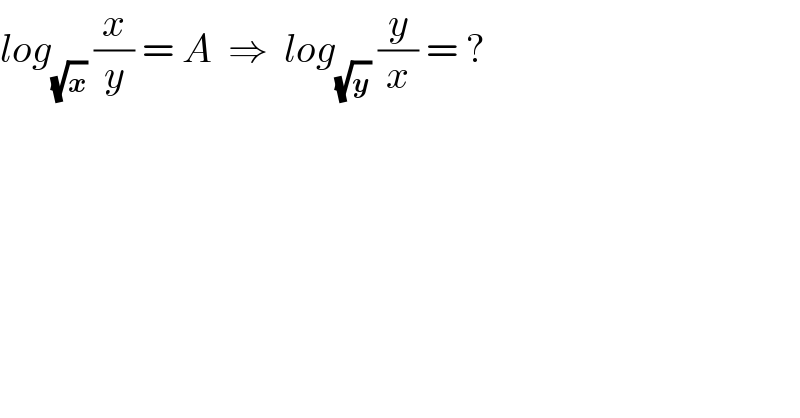
Answered by Ar Brandon last updated on 29/Jul/21
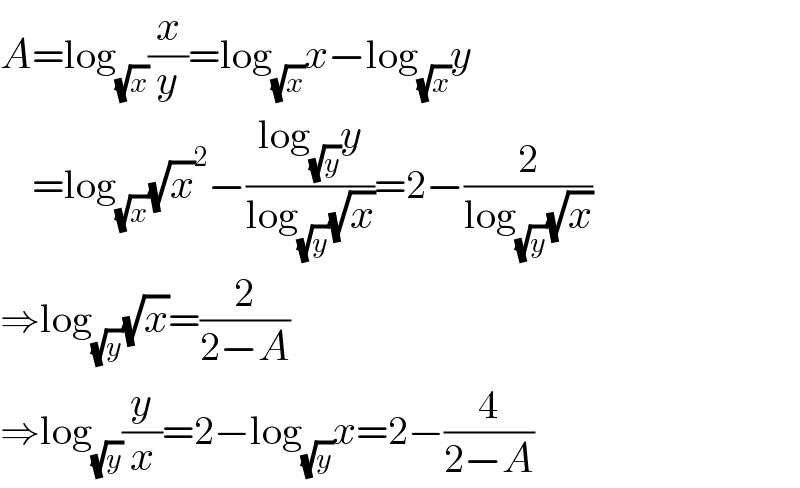
Commented by puissant last updated on 29/Jul/21
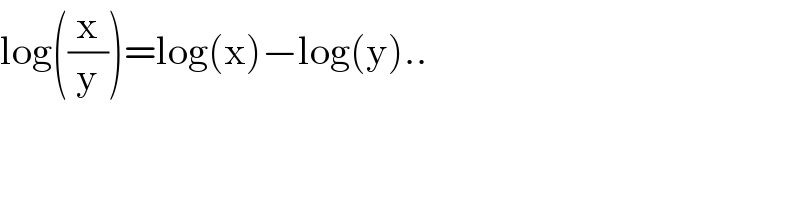
Commented by Ar Brandon last updated on 29/Jul/21
Commented by mathdanisur last updated on 29/Jul/21

Commented by Ar Brandon last updated on 29/Jul/21

Answered by EDWIN88 last updated on 29/Jul/21
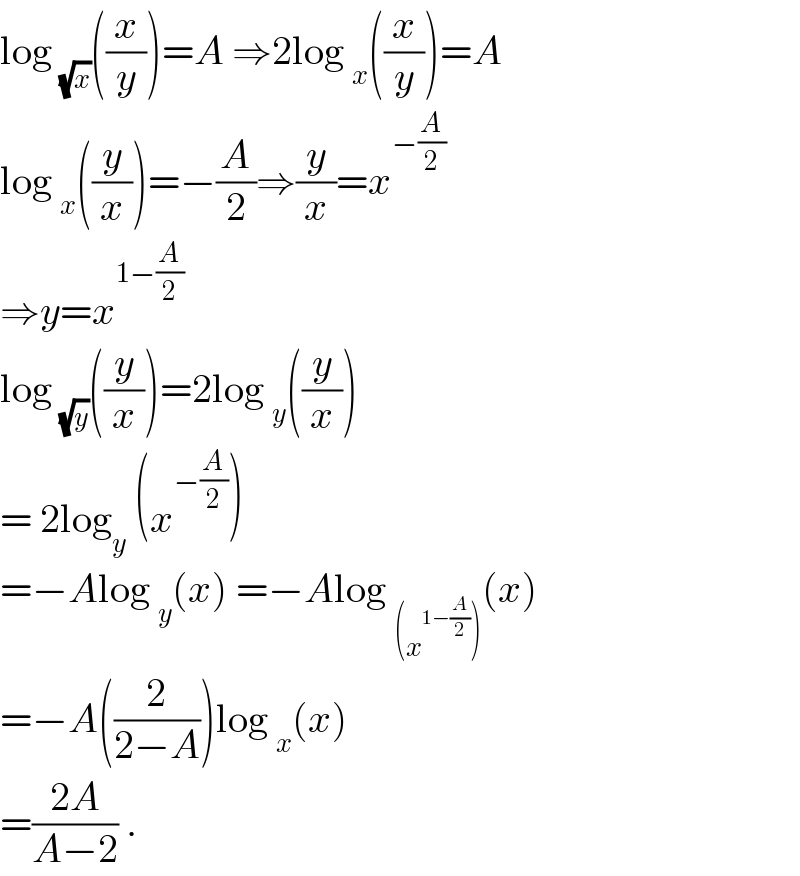
Commented by mathdanisur last updated on 29/Jul/21

