Question Number 49003 by mondodotto@gmail.com last updated on 01/Dec/18
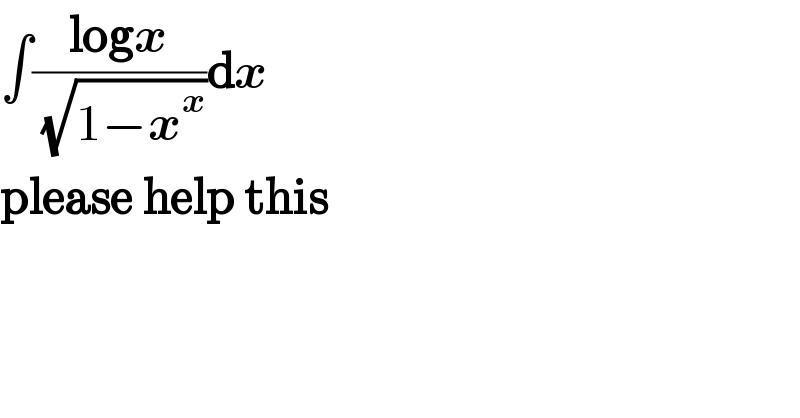
$$\int\frac{\boldsymbol{\mathrm{log}{x}}}{\:\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\boldsymbol{{x}}} }}\boldsymbol{\mathrm{d}{x}} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{help}}\:\boldsymbol{\mathrm{this}} \\ $$
Commented by maxmathsup by imad last updated on 01/Dec/18

$${I}\:=\int\:\:\:\frac{{ln}\left({x}\right)}{\:\sqrt{\mathrm{1}−{e}^{{xln}\left({x}\right)} }}{dx}\:\:{changement}\:{xln}\left({x}\right)={t}\:{give}\:\left({ln}\left({x}\right)+\mathrm{1}\right){dx}\:={dt} \\ $$$${I}\:=\int\:\frac{{ln}\left({x}\right)+\mathrm{1}−\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{{x}} }}{dx}\:=\int\:\:\frac{{ln}\left({x}\right)+\mathrm{1}}{\:\sqrt{\mathrm{1}−{e}^{{xlnx}} }}{dx}\:−\int\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{{x}} }} \\ $$$$=\int\:\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}}}\:\:−\int\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{{x}} }}\:=−\mathrm{2}\sqrt{\mathrm{1}−{t}}\:−\int\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{{x}} }}\:=−\mathrm{2}\sqrt{\mathrm{1}−{x}^{{x}} }\:−\int\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{{x}} }} \\ $$$${let}\:{find}\:\int\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{{x}} }}\:\:{at}\:{form}\:{of}\:{serie}\:{due}\:{to}\:\:\mathrm{0}<{x}^{{x}} <\mathrm{1} \\ $$$${we}\:{have}\:\left(\mathrm{1}+{u}\right)^{\alpha} \:=\mathrm{1}+\frac{\alpha{u}}{\mathrm{1}!}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}!}\:{u}^{\mathrm{2}} \:+….+\frac{\alpha\left(\alpha−\mathrm{1}\right)…\left(\alpha−{n}+\mathrm{1}\right)}{{n}!}\:{u}^{{n}} \:+…\:\Rightarrow \\ $$$$\left(\mathrm{1}−{u}\right)^{\alpha} \:=\mathrm{1}−\alpha{u}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}!}\:{u}^{\mathrm{2}} \:\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)…\left(\alpha−{n}+\mathrm{1}\right)}{{n}!}\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \:+…\:\Rightarrow \\ $$$$\left(\mathrm{1}−{x}^{{x}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:{x}^{{x}} \:\:+\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{2}!}\:{x}^{\mathrm{2}{x}} \:+…\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)…\left(−\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)}{{n}!}\:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{nx}} +… \\ $$$$\Rightarrow\int\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{{x}} }}\:={x}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int\:{x}^{{x}} {dx}\:+\int\:\:\frac{\mathrm{3}}{\mathrm{4}\:\mathrm{2}!}\:{x}^{\mathrm{2}{x}} {dx}\:+… \\ $$$$+\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)….\left(−\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)}{{n}!}\:\left(−\mathrm{1}\right)^{{n}\:} \:\int\:\:\:{x}^{{nx}} {dx}+…. \\ $$
Commented by MJS last updated on 01/Dec/18
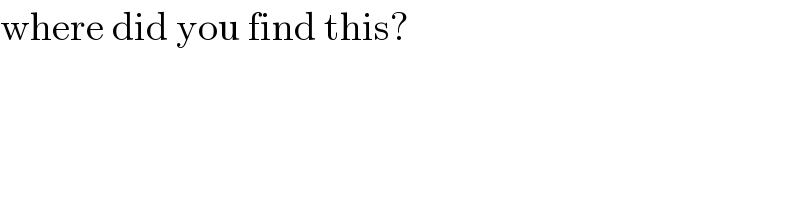
$$\mathrm{where}\:\mathrm{did}\:\mathrm{you}\:\mathrm{find}\:\mathrm{this}? \\ $$
