Question Number 176603 by a.lgnaoui last updated on 23/Sep/22
$${look}\:{the}\:{anser} \\ $$
Commented by a.lgnaoui last updated on 23/Sep/22
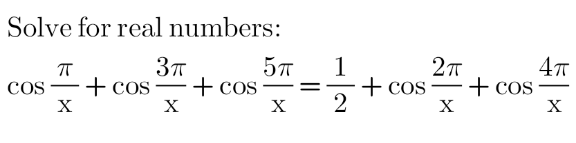
Commented by mr W last updated on 23/Sep/22
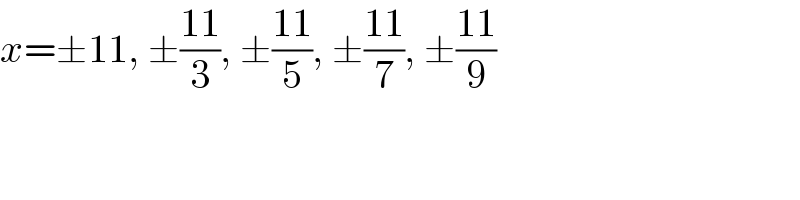
$${x}=\pm\mathrm{11},\:\pm\frac{\mathrm{11}}{\mathrm{3}},\:\pm\frac{\mathrm{11}}{\mathrm{5}},\:\pm\frac{\mathrm{11}}{\mathrm{7}},\:\pm\frac{\mathrm{11}}{\mathrm{9}} \\ $$
Commented by Shrinava last updated on 23/Sep/22
$$\mathrm{How}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{please} \\ $$
Commented by MJS_new last updated on 23/Sep/22
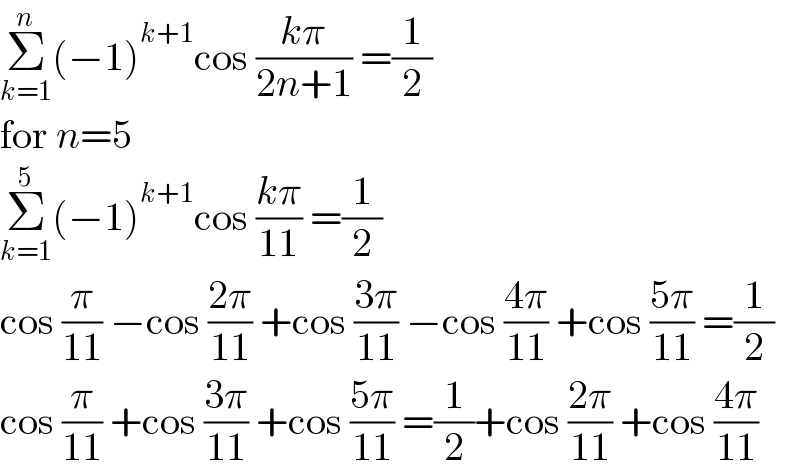
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \mathrm{cos}\:\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{for}\:{n}=\mathrm{5} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{5}} {\sum}}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \mathrm{cos}\:\frac{{k}\pi}{\mathrm{11}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{11}}\:−\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{11}}\:+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{11}}\:−\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{11}}\:+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{11}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{11}}\:+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{11}}\:+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{11}}\:=\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{11}}\:+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{11}} \\ $$
Commented by MJS_new last updated on 23/Sep/22
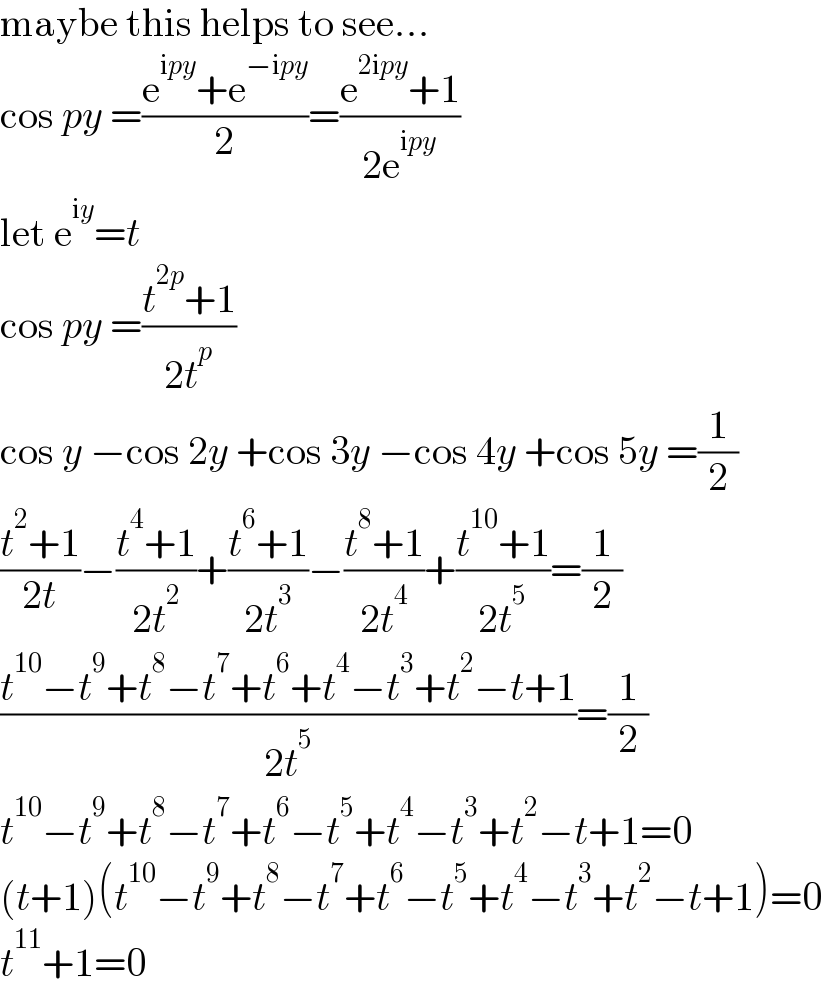
$$\mathrm{maybe}\:\mathrm{this}\:\mathrm{helps}\:\mathrm{to}\:\mathrm{see}… \\ $$$$\mathrm{cos}\:{py}\:=\frac{\mathrm{e}^{\mathrm{i}{py}} +\mathrm{e}^{−\mathrm{i}{py}} }{\mathrm{2}}=\frac{\mathrm{e}^{\mathrm{2i}{py}} +\mathrm{1}}{\mathrm{2e}^{\mathrm{i}{py}} } \\ $$$$\mathrm{let}\:\mathrm{e}^{\mathrm{i}{y}} ={t} \\ $$$$\mathrm{cos}\:{py}\:=\frac{{t}^{\mathrm{2}{p}} +\mathrm{1}}{\mathrm{2}{t}^{{p}} } \\ $$$$\mathrm{cos}\:{y}\:−\mathrm{cos}\:\mathrm{2}{y}\:+\mathrm{cos}\:\mathrm{3}{y}\:−\mathrm{cos}\:\mathrm{4}{y}\:+\mathrm{cos}\:\mathrm{5}{y}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{t}}−\frac{{t}^{\mathrm{4}} +\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }+\frac{{t}^{\mathrm{6}} +\mathrm{1}}{\mathrm{2}{t}^{\mathrm{3}} }−\frac{{t}^{\mathrm{8}} +\mathrm{1}}{\mathrm{2}{t}^{\mathrm{4}} }+\frac{{t}^{\mathrm{10}} +\mathrm{1}}{\mathrm{2}{t}^{\mathrm{5}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{t}^{\mathrm{10}} −{t}^{\mathrm{9}} +{t}^{\mathrm{8}} −{t}^{\mathrm{7}} +{t}^{\mathrm{6}} +{t}^{\mathrm{4}} −{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −{t}+\mathrm{1}}{\mathrm{2}{t}^{\mathrm{5}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${t}^{\mathrm{10}} −{t}^{\mathrm{9}} +{t}^{\mathrm{8}} −{t}^{\mathrm{7}} +{t}^{\mathrm{6}} −{t}^{\mathrm{5}} +{t}^{\mathrm{4}} −{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −{t}+\mathrm{1}=\mathrm{0} \\ $$$$\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{10}} −{t}^{\mathrm{9}} +{t}^{\mathrm{8}} −{t}^{\mathrm{7}} +{t}^{\mathrm{6}} −{t}^{\mathrm{5}} +{t}^{\mathrm{4}} −{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$${t}^{\mathrm{11}} +\mathrm{1}=\mathrm{0} \\ $$
Commented by Tawa11 last updated on 23/Sep/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by a.lgnaoui last updated on 23/Sep/22
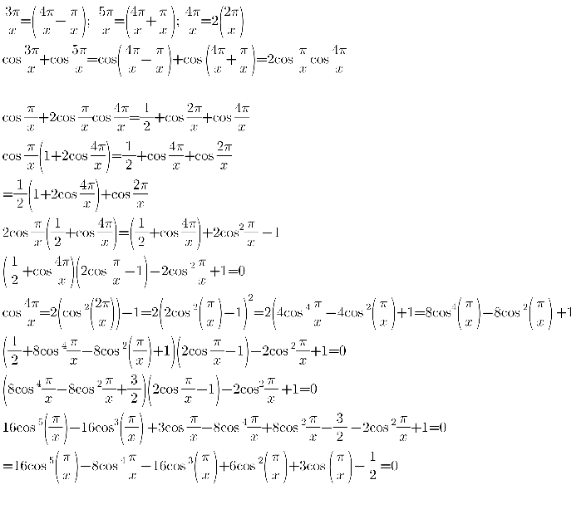
Answered by a.lgnaoui last updated on 23/Sep/22

