Question Number 17775 by gourav~ last updated on 10/Jul/17
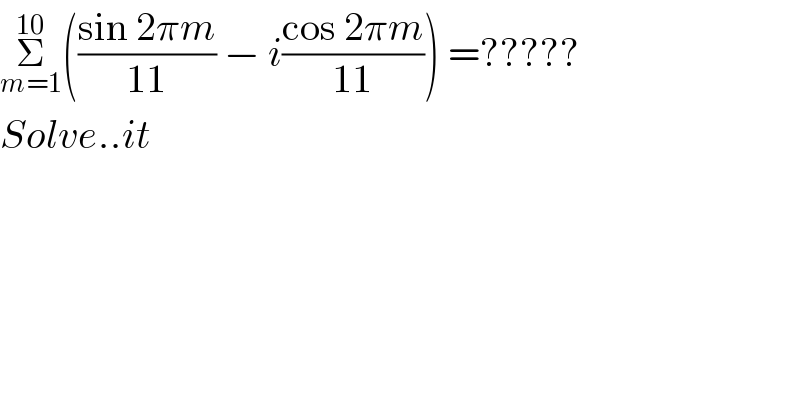
$$\underset{{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(\frac{\mathrm{sin}\:\mathrm{2}\pi{m}}{\mathrm{11}}\:−\:{i}\frac{\mathrm{cos}\:\mathrm{2}\pi{m}}{\mathrm{11}}\right)\:=????? \\ $$$${Solve}..{it} \\ $$$$ \\ $$
Answered by alex041103 last updated on 10/Jul/17
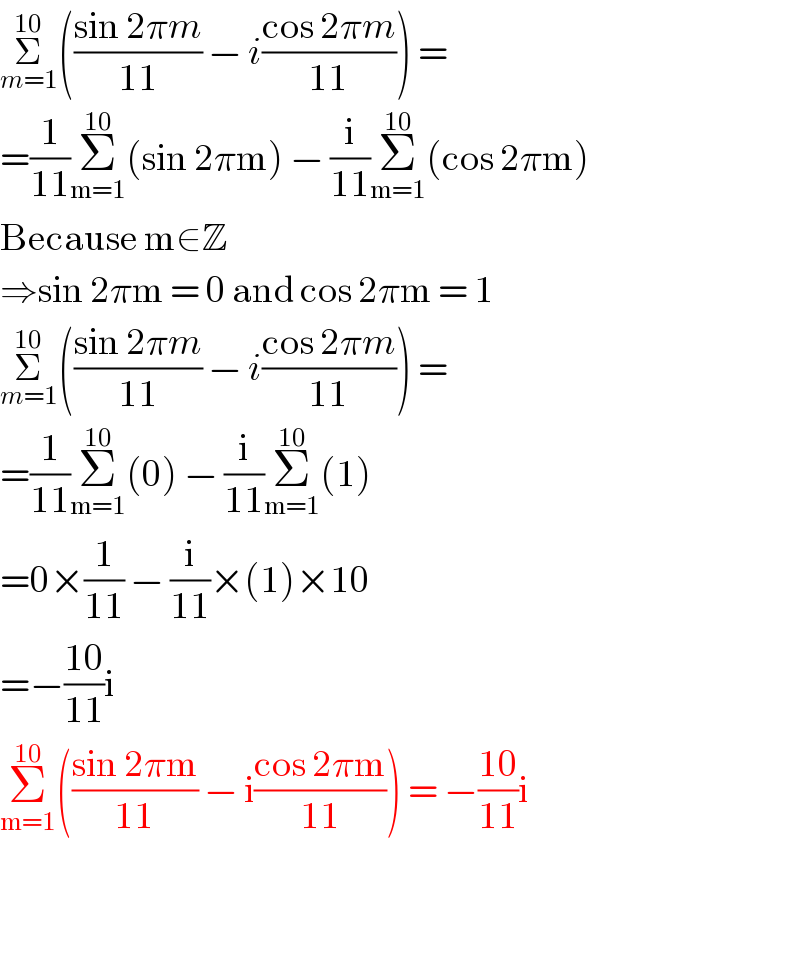
$$\underset{{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(\frac{\mathrm{sin}\:\mathrm{2}\pi{m}}{\mathrm{11}}\:−\:{i}\frac{\mathrm{cos}\:\mathrm{2}\pi{m}}{\mathrm{11}}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{11}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(\mathrm{sin}\:\mathrm{2}\pi\mathrm{m}\right)\:−\:\frac{\mathrm{i}}{\mathrm{11}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(\mathrm{cos}\:\mathrm{2}\pi\mathrm{m}\right) \\ $$$$\mathrm{Because}\:\mathrm{m}\in\mathbb{Z}\: \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}\pi\mathrm{m}\:=\:\mathrm{0}\:\mathrm{and}\:\mathrm{cos}\:\mathrm{2}\pi\mathrm{m}\:=\:\mathrm{1} \\ $$$$\underset{{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(\frac{\mathrm{sin}\:\mathrm{2}\pi{m}}{\mathrm{11}}\:−\:{i}\frac{\mathrm{cos}\:\mathrm{2}\pi{m}}{\mathrm{11}}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{11}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(\mathrm{0}\right)\:−\:\frac{\mathrm{i}}{\mathrm{11}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(\mathrm{1}\right) \\ $$$$=\mathrm{0}×\frac{\mathrm{1}}{\mathrm{11}}\:−\:\frac{\mathrm{i}}{\mathrm{11}}×\left(\mathrm{1}\right)×\mathrm{10} \\ $$$$=−\frac{\mathrm{10}}{\mathrm{11}}\mathrm{i} \\ $$$$\underset{\mathrm{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(\frac{\mathrm{sin}\:\mathrm{2}\pi\mathrm{m}}{\mathrm{11}}\:−\:\mathrm{i}\frac{\mathrm{cos}\:\mathrm{2}\pi\mathrm{m}}{\mathrm{11}}\right)\:=\:−\frac{\mathrm{10}}{\mathrm{11}}\mathrm{i} \\ $$$$ \\ $$$$ \\ $$
Answered by ajfour last updated on 10/Jul/17
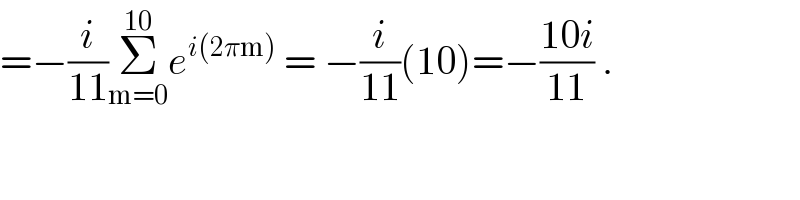
$$=−\frac{{i}}{\mathrm{11}}\underset{\mathrm{m}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}{e}^{{i}\left(\mathrm{2}\pi\mathrm{m}\right)} \:=\:−\frac{{i}}{\mathrm{11}}\left(\mathrm{10}\right)=−\frac{\mathrm{10}{i}}{\mathrm{11}}\:. \\ $$
