Question Number 147543 by alcohol last updated on 21/Jul/21

$$\underset{{m}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{m}} \\ $$
Answered by Canebulok last updated on 21/Jul/21

$$\: \\ $$$$\boldsymbol{{Solution}}: \\ $$$${let}: \\ $$$$\Rightarrow\:\underset{{m}=\mathrm{1}} {\overset{{n}} {\prod}}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{m}} \:=\:\varphi \\ $$$${By}\:{taking}\:{the}\:{natural}\:{log}\:{of}\:{both}\:{sides}, \\ $$$$\Rightarrow\:\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\:{Ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\centerdot\left({m}\right)\:=\:{Ln}\left(\varphi\right) \\ $$$$\Rightarrow\:{Ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\centerdot\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\:\left({m}\right)\:=\:{Ln}\left(\varphi\right) \\ $$$$\Rightarrow\:{Ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\centerdot\left(\frac{{n}\centerdot\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right)\:=\:{Ln}\left(\varphi\right) \\ $$$$\because \\ $$$$\Rightarrow\:\varphi\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{{n}\centerdot\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$\: \\ $$
Answered by gsk2684 last updated on 21/Jul/21
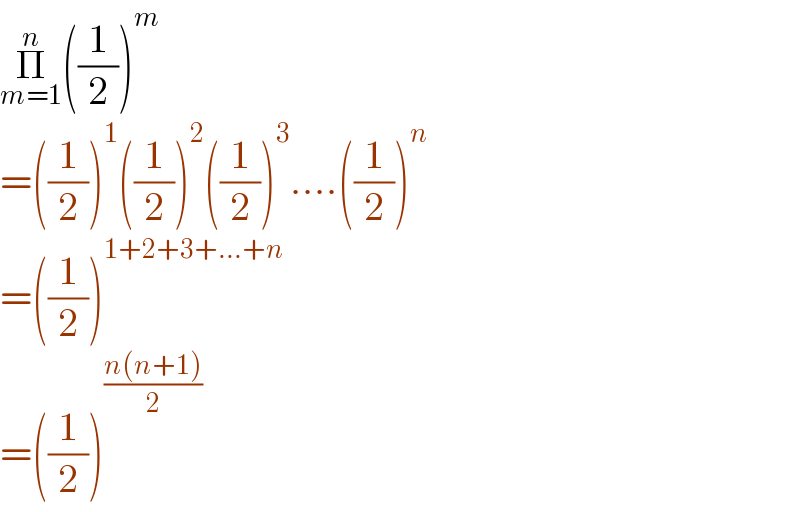
$$\underset{{m}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{m}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} ….\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{n}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \\ $$
