Question Number 121119 by benjo_mathlover last updated on 05/Nov/20
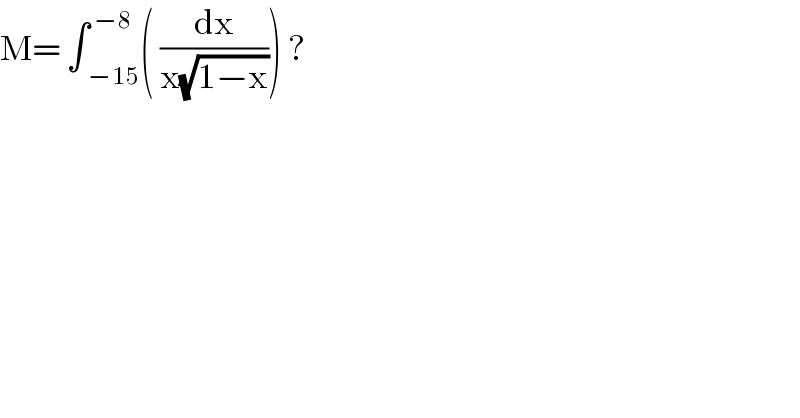
$$\mathrm{M}=\:\int\underset{−\mathrm{15}} {\overset{−\mathrm{8}} {\:}}\left(\:\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}}}\right)\:?\: \\ $$
Answered by liberty last updated on 05/Nov/20
![M =∫_(−15) ^(−8) (dx/(x^2 (√(x^(−1) −1)))) let u = x^(−1) −1 ⇒du=−x^(−2) dx → { ((u=−(9/8))),((u=−((16)/(15)))) :} M=−∫_(−16/15) ^(−9/8) (du/u^(1/2) ) = −2(√u) ]_(−16/15) ^(−9/8) = −((3i)/( (√2))) −(−((8i)/( (√(15)))))=((8/( (√(15))))−(3/( (√2))))i](https://www.tinkutara.com/question/Q121120.png)
$$\mathrm{M}\:=\underset{−\mathrm{15}} {\overset{−\mathrm{8}} {\int}}\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{−\mathrm{1}} −\mathrm{1}}} \\ $$$$\mathrm{let}\:\mathrm{u}\:=\:\mathrm{x}^{−\mathrm{1}} −\mathrm{1}\:\Rightarrow\mathrm{du}=−\mathrm{x}^{−\mathrm{2}} \:\mathrm{dx}\:\rightarrow\begin{cases}{\mathrm{u}=−\frac{\mathrm{9}}{\mathrm{8}}}\\{\mathrm{u}=−\frac{\mathrm{16}}{\mathrm{15}}}\end{cases} \\ $$$$\left.\mathrm{M}=−\underset{−\mathrm{16}/\mathrm{15}} {\overset{−\mathrm{9}/\mathrm{8}} {\int}}\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{1}/\mathrm{2}} }\:=\:−\mathrm{2}\sqrt{\mathrm{u}}\:\right]_{−\mathrm{16}/\mathrm{15}} ^{−\mathrm{9}/\mathrm{8}} \\ $$$$=\:−\frac{\mathrm{3}{i}}{\:\sqrt{\mathrm{2}}}\:−\left(−\frac{\mathrm{8}{i}}{\:\sqrt{\mathrm{15}}}\right)=\left(\frac{\mathrm{8}}{\:\sqrt{\mathrm{15}}}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right){i} \\ $$
Answered by 675480065 last updated on 05/Nov/20
![u^2 =1−x ⇒ du=−dx {x=1−u^2 } U=∫_u_1 ^( u_2 ) (du/((u^2 −1)u)) =∫_u_1 ^( u_2 ) (du/((u−1)(u+1)u)) M=(1/2)ln∣(√(1−x))+1∣+(1/2)ln∣(√(1−x))−1∣−ln∣(√(1−x))∣]_(−15) ^(−8) M=[ln∣(x^2 /( (√(1−x))))∣]_(−15) ^(−8) =ln(((64)/3)×(4/(225)))](https://www.tinkutara.com/question/Q121121.png)
$$\mathrm{u}^{\mathrm{2}} =\mathrm{1}−\mathrm{x}\:\Rightarrow\:\mathrm{du}=−\mathrm{dx}\:\left\{\mathrm{x}=\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right\} \\ $$$$\mathrm{U}=\int_{\mathrm{u}_{\mathrm{1}} } ^{\:\mathrm{u}_{\mathrm{2}} } \frac{\mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{u}}\:=\int_{\mathrm{u}_{\mathrm{1}} } ^{\:\mathrm{u}_{\mathrm{2}} } \frac{\mathrm{du}}{\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{u}+\mathrm{1}\right)\mathrm{u}} \\ $$$$\left.\mathrm{M}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\sqrt{\mathrm{1}−\mathrm{x}}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\sqrt{\mathrm{1}−\mathrm{x}}−\mathrm{1}\mid−\mathrm{ln}\mid\sqrt{\mathrm{1}−\mathrm{x}}\mid\right]_{−\mathrm{15}} ^{−\mathrm{8}} \\ $$$$\mathrm{M}=\left[\mathrm{ln}\mid\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\mathrm{x}}}\mid\right]_{−\mathrm{15}} ^{−\mathrm{8}} =\mathrm{ln}\left(\frac{\mathrm{64}}{\mathrm{3}}×\frac{\mathrm{4}}{\mathrm{225}}\right) \\ $$
Answered by MJS_new last updated on 05/Nov/20
![∫(dx/(x(√(1−x))))= [t=((1+(√(1−x)))/( (√x))) → dx=−2(x−1+(√(1−x)))(√x)dt] =−2∫(dt/t)=−2ln ∣t∣ ⇒ M=ln (5/6)](https://www.tinkutara.com/question/Q121124.png)
$$\int\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}}}{\:\sqrt{{x}}}\:\rightarrow\:{dx}=−\mathrm{2}\left({x}−\mathrm{1}+\sqrt{\mathrm{1}−{x}}\right)\sqrt{{x}}{dt}\right] \\ $$$$=−\mathrm{2}\int\frac{{dt}}{{t}}=−\mathrm{2ln}\:\mid{t}\mid\:\Rightarrow\:{M}=\mathrm{ln}\:\frac{\mathrm{5}}{\mathrm{6}} \\ $$
Answered by Bird last updated on 05/Nov/20
![M=∫_(−15) ^(−8) (dx/(x(√(1−x)))) changement (√(1−x))=t give 1−x=t^2 ⇒x=1−t^2 ⇒M =∫_4 ^3 ((−2tdt)/((1−t^2 )t)) =2∫_3 ^4 (dt/(1−t^2 )) =∫_3 ^4 ((1/(1−t))+(1/(1+t)))dt =[ln∣((1+t)/(1−t))∣]_3 ^4 =ln((5/3))−ln((4/2)) =ln5 −ln3−ln2 =ln5−ln6](https://www.tinkutara.com/question/Q121197.png)
$${M}=\int_{−\mathrm{15}} ^{−\mathrm{8}} \:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}}}\:{changement} \\ $$$$\sqrt{\mathrm{1}−{x}}={t}\:{give}\:\mathrm{1}−{x}={t}^{\mathrm{2}} \:\Rightarrow{x}=\mathrm{1}−{t}^{\mathrm{2}} \\ $$$$\Rightarrow{M}\:=\int_{\mathrm{4}} ^{\mathrm{3}} \:\:\frac{−\mathrm{2}{tdt}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right){t}}\:=\mathrm{2}\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{3}} ^{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$=\left[{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\right]_{\mathrm{3}} ^{\mathrm{4}} \:={ln}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)−{ln}\left(\frac{\mathrm{4}}{\mathrm{2}}\right) \\ $$$$={ln}\mathrm{5}\:−{ln}\mathrm{3}−{ln}\mathrm{2}\:={ln}\mathrm{5}−{ln}\mathrm{6} \\ $$
