Question Number 62942 by Tawa1 last updated on 27/Jun/19
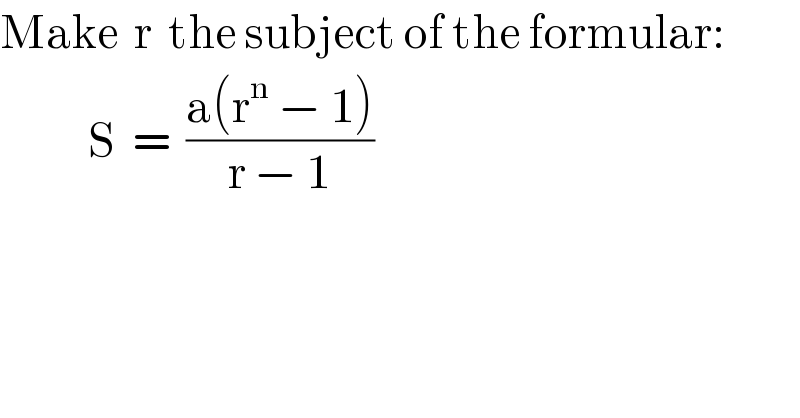
Commented by Tawa1 last updated on 27/Jun/19
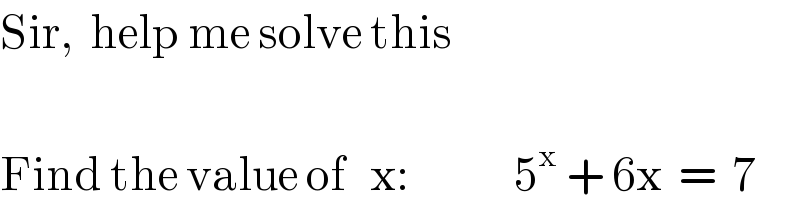
Commented by Tawa1 last updated on 27/Jun/19
Commented by mr W last updated on 27/Jun/19

Commented by Tawa1 last updated on 27/Jun/19

Commented by mr W last updated on 27/Jun/19
![5^x +6x=7 5^x =6((7/6)−x) ((7/6)−x)5^(−x) =(1/6) ((7/6)−x)5^((7/6)−x) =(1/6)×5^(7/6) ((7/6)−x)e^(((7/6)−x)ln 5) =(1/6)×5^(7/6) [((7/6)−x)ln 5]e^(((7/6)−x)ln 5) =(1/6)×5^(7/6) ×ln 5 ⇒((7/6)−x)ln 5=W((1/6)×5^(7/6) ×ln 5) ⇒x=(7/6)−(1/(ln 5))W((1/6)×5^(7/6) ×ln 5) ⇒≈(7/6)−((0.7933)/(ln 5))=0.6737](https://www.tinkutara.com/question/Q62963.png)
Commented by kaivan.ahmadi last updated on 27/Jun/19

Commented by Hope last updated on 27/Jun/19
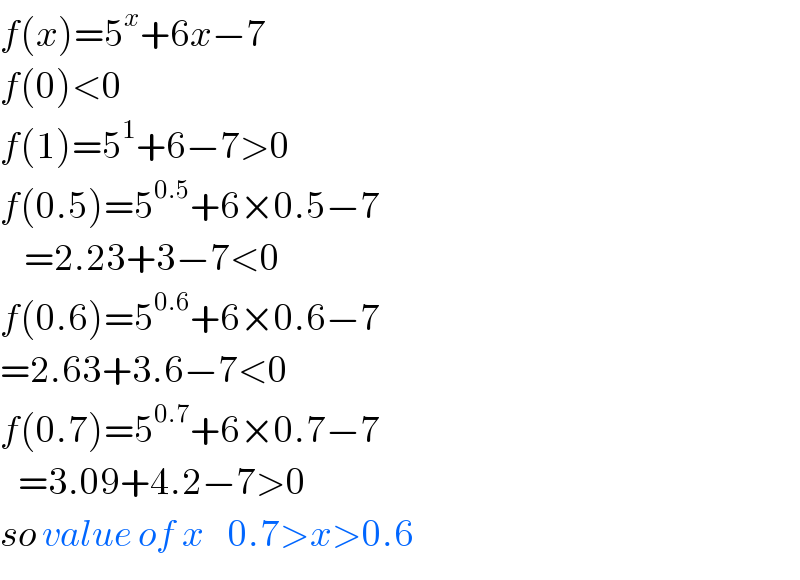
Commented by Tawa1 last updated on 27/Jun/19
Commented by Tawa1 last updated on 27/Jun/19
Commented by Tawa1 last updated on 27/Jun/19
Answered by peter frank last updated on 27/Jun/19
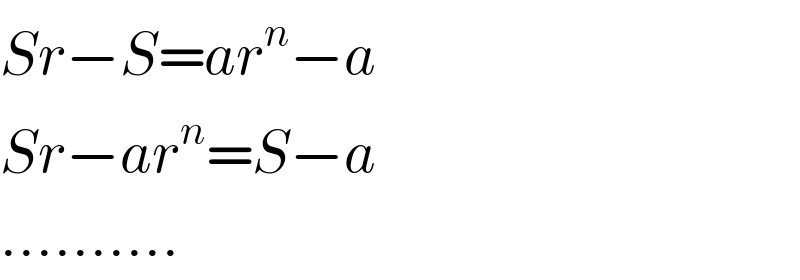
Commented by Tawa1 last updated on 27/Jun/19

