Question Number 115507 by mnjuly1970 last updated on 26/Sep/20
![.... ...matematical analysis... prove that ::: a>0 :: [((i : ∫_(0 ) ^( ∞) ((sin^2 (ax))/x^(3/2) ) dx= (√(πa)))),((ii: ∫_0 ^( ∞) ((sin^3 (ax))/( (√x))) dx = ((−1+3(√(3 )))/4) (√((π/(6a)) )) )) ] ...m.n.july.1970...](https://www.tinkutara.com/question/Q115507.png)
$$\:\:\:\:\:\:\:\:\:\:\:….\:\:\:…{matematical}\:{analysis}…\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:{prove}\:{that}\:::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}>\mathrm{0}\:::\:\:\:\begin{bmatrix}{{i}\::\:\:\int_{\mathrm{0}\:} ^{\:\infty} \frac{{sin}^{\mathrm{2}} \left({ax}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{dx}=\:\sqrt{\pi{a}}}\\{{ii}:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}^{\mathrm{3}} \left({ax}\right)}{\:\sqrt{{x}}}\:{dx}\:=\:\frac{−\mathrm{1}+\mathrm{3}\sqrt{\mathrm{3}\:}}{\mathrm{4}}\:\sqrt{\frac{\pi}{\mathrm{6}{a}}\:\:}\:}\end{bmatrix} \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{m}.{n}.{july}.\mathrm{1970}… \\ $$$$ \\ $$
Answered by mathdave last updated on 26/Sep/20

$$\left(\mathrm{1}\right)\:{let}\:{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{2}} \left({ax}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left(\mathrm{2}{ax}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{\pi{a}^{{n}−\mathrm{1}} }{\mathrm{2}\Gamma\left({n}\right)\mathrm{sin}\left(\frac{\pi{n}}{\mathrm{2}}\right)}\left({call}\:{maz}\:{identity}\right) \\ $$$${I}=\frac{\pi\left(\mathrm{2}{a}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi.}\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)}=\frac{\sqrt{{a}\pi}.\sqrt{\mathrm{2}}}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\sqrt{{a}\pi}.\sqrt{\mathrm{2}}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\mathrm{2}\:\sqrt{{a}\pi} \\ $$$$\because\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{2}} \left({ax}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx}=\mathrm{2}\sqrt{{a}\pi}\:\:\:\:\:\:\:\:\:\:\:\:{Q}.{E}.{D} \\ $$$$\left(\mathrm{2}\right)\:{let}\:{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{3}} \left({ax}\right)}{\:\sqrt{{x}}}{dx} \\ $$$${but}\:\mathrm{sin}\left(\mathrm{3}{x}\right)=\mathrm{3sin}{x}−\mathrm{4sin}^{\mathrm{3}} {x},\mathrm{sin}^{\mathrm{3}} {x}=\frac{\mathrm{3sin}{x}−\mathrm{sin}\left(\mathrm{3}{x}\right)}{\mathrm{4}} \\ $$$${I}=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left({ax}\right)}{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }{dx}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left(\mathrm{3}{ax}\right)}{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }{dx} \\ $$$${I}=\frac{\mathrm{3}}{\mathrm{4}}.\frac{\pi{a}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}\sqrt{\pi}.\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}−\frac{\mathrm{1}}{\mathrm{4}}.\frac{\pi\left(\mathrm{3}{a}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}\sqrt{\pi}.\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\mathrm{3}}{\mathrm{4}}.\frac{\sqrt{\pi}.\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{{a}}}−\frac{\mathrm{1}}{\mathrm{4}}.\frac{\sqrt{\pi}.\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{3}{a}}} \\ $$$${I}=\:\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}\sqrt{\mathrm{2}{a}}}−\frac{\sqrt{\pi}}{\mathrm{4}\sqrt{\mathrm{6}{a}}}\:=\frac{\mathrm{3}\sqrt{\mathrm{3}}.\sqrt{\pi}−\sqrt{\pi}}{\mathrm{4}\sqrt{\mathrm{6}{a}}}=\frac{\left(−\mathrm{1}+\mathrm{3}\sqrt{\mathrm{3}}\right)\sqrt{\pi}}{\mathrm{4}\sqrt{\mathrm{6}{a}}}=\frac{−\mathrm{1}+\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\sqrt{\frac{\pi}{\mathrm{6}{a}}}\:\:\:\:\:\:\:\:? \\ $$$$\because\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{3}} \left({ax}\right)}{\:\sqrt{{x}}}{dx}=\frac{−\mathrm{1}+\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\sqrt{\frac{\pi}{\mathrm{6}{a}}}\:\:\:\:\:\:\:\:\:\:\:{Q}.{E}.{D} \\ $$$${by}\:{mathdave}\left(\mathrm{26}/\mathrm{09}/\mathrm{2020}\right) \\ $$
Commented by mnjuly1970 last updated on 26/Sep/20
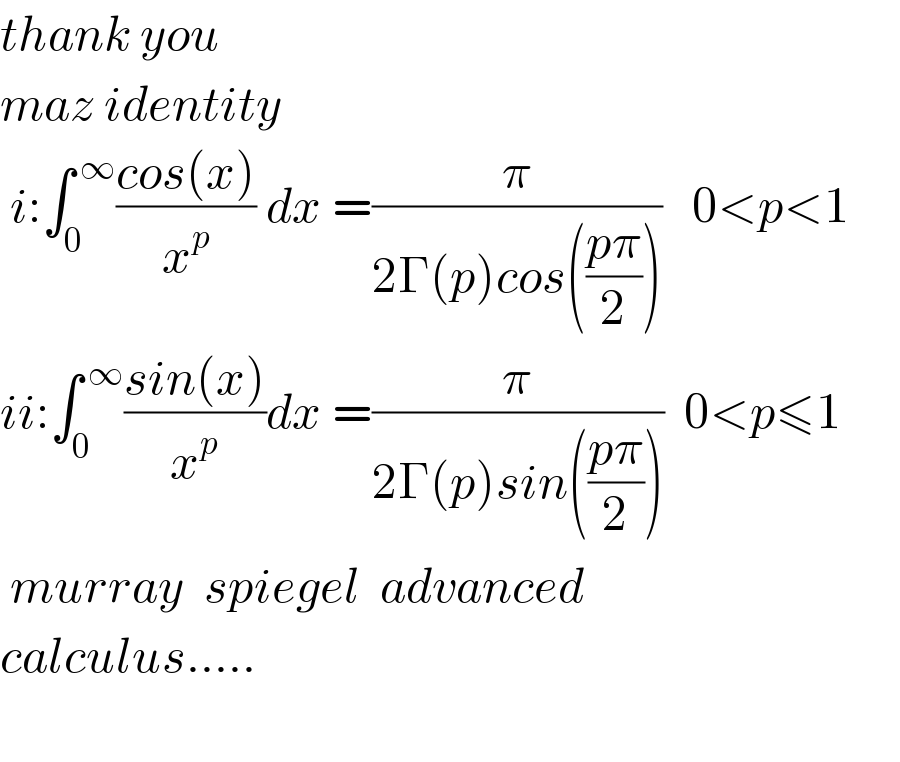
$${thank}\:{you} \\ $$$${maz}\:{identity} \\ $$$$\:{i}:\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left({x}\right)}{{x}^{{p}} }\:{dx}\:=\frac{\pi}{\mathrm{2}\Gamma\left({p}\right){cos}\left(\frac{{p}\pi}{\mathrm{2}}\right)}\:\:\:\mathrm{0}<{p}<\mathrm{1}\:\:\:\:\: \\ $$$${ii}:\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right)}{{x}^{{p}} }{dx}\:=\frac{\pi}{\mathrm{2}\Gamma\left({p}\right){sin}\left(\frac{{p}\pi}{\mathrm{2}}\right)}\:\:\mathrm{0}<{p}\leqslant\mathrm{1} \\ $$$$\:{murray}\:\:{spiegel}\:\:{advanced}\: \\ $$$${calculus}….. \\ $$$$\:\: \\ $$
Commented by mnjuly1970 last updated on 26/Sep/20
$${thanks}\:{a}\:{lot}\:{mr}\:{dave} \\ $$
Answered by Bird last updated on 28/Sep/20
![I=∫_0 ^∞ ((sin^2 (ax))/x^(3/2) ) dx ⇒I =_(ax =t) ∫_0 ^∞ ((sin^2 t)/(((t/a))^(3/2) ))×(dt/a) =a^((3/2)−1) ∫_0 ^∞ ((sin^2 t)/t^(3/2) )dt ==(√(a ))∫_0 ^∞ ((sin^2 t )/t^(3/2) )dt by parts ∫_0 ^∞ t^(−(3/(2 ))) sin^2 t dt =[(1/(1−(3/2))) t^(1−(3/2)) sin^2 t]_0 ^∞ −∫_0 ^∞ −2 t^(−(1/2)) ×2sint cost dt =2 ∫_0 ^∞ ((sin(2t))/( (√t))) dt =_((√t)=u) 2∫_0 ^∞ ((sin(2u^2 ))/u)(2u)du =4 ∫_0 ^∞ sin(2u^2 )du =−4 Im(∫_0 ^∞ e^(−2iu^2 ) du) ∫_0 ^∞ e^(−((√(2i))u)^2 ) du =_((√(2i))u=z) ∫_0 ^∞ e^(−z^2 ) (dz/( (√(2i)))) =(1/( (√2)))e^(−((iπ)/4)) ×((√π)/2) =((√π)/(2(√2)))(((√2)/2)−((i(√2))/2)) =((√π)/4)−((i(√π))/4) ⇒ ∫_0 ^∞ t^(−(3/2)) sin^2 t dt =−4(−((√π)/4))=(√π) ⇒I =(√a)×(√π) =(√(πa))](https://www.tinkutara.com/question/Q115724.png)
$${I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} \left({ax}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{dx} \\ $$$$\Rightarrow{I}\:=_{{ax}\:={t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {t}}{\left(\frac{{t}}{{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }×\frac{{dt}}{{a}} \\ $$$$={a}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {t}}{{t}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dt} \\ $$$$==\sqrt{{a}\:}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}^{\mathrm{2}} {t}\:}{{t}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dt}\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{t}^{−\frac{\mathrm{3}}{\mathrm{2}\:}} \:{sin}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}}\:{t}^{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}} \:{sin}^{\mathrm{2}} {t}\right]_{\mathrm{0}} ^{\infty} \\ $$$$−\int_{\mathrm{0}} ^{\infty} \:\:−\mathrm{2}\:{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:×\mathrm{2}{sint}\:{cost}\:{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left(\mathrm{2}{t}\right)}{\:\sqrt{{t}}}\:{dt} \\ $$$$=_{\sqrt{{t}}={u}} \:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left(\mathrm{2}{u}^{\mathrm{2}} \right)}{{u}}\left(\mathrm{2}{u}\right){du} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:{sin}\left(\mathrm{2}{u}^{\mathrm{2}} \right){du} \\ $$$$=−\mathrm{4}\:{Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{iu}^{\mathrm{2}} } {du}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\sqrt{\mathrm{2}{i}}{u}\right)^{\mathrm{2}} } {du}\:=_{\sqrt{\mathrm{2}{i}}{u}={z}} \:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{z}^{\mathrm{2}} } \frac{{dz}}{\:\sqrt{\mathrm{2}{i}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:×\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{{i}\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{4}}−\frac{{i}\sqrt{\pi}}{\mathrm{4}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} {t}^{−\frac{\mathrm{3}}{\mathrm{2}}} {sin}^{\mathrm{2}} {t}\:{dt}\:=−\mathrm{4}\left(−\frac{\sqrt{\pi}}{\mathrm{4}}\right)=\sqrt{\pi} \\ $$$$\Rightarrow{I}\:=\sqrt{{a}}×\sqrt{\pi}\:=\sqrt{\pi{a}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 28/Sep/20

$${thank}\:{you}\:{so}\:{much}\:\:{sir}\:{math} \\ $$$${bird}.. \\ $$
