Max-and-min-P-2-x-3-y-subject-to-constraint-x-2-9-y-2-25-1-x-2-y-2-

Question Number 172253 by cortano1 last updated on 25/Jun/22

M a x a n d m i n P = \sqrt{2} x + \sqrt{3} y

s u b j e c t t o c o n s t r a i n t

\frac{x^{2}}{9} + \frac{y^{2}}{25} ⩽ 1 ⩽ x^{2} + y^{2}

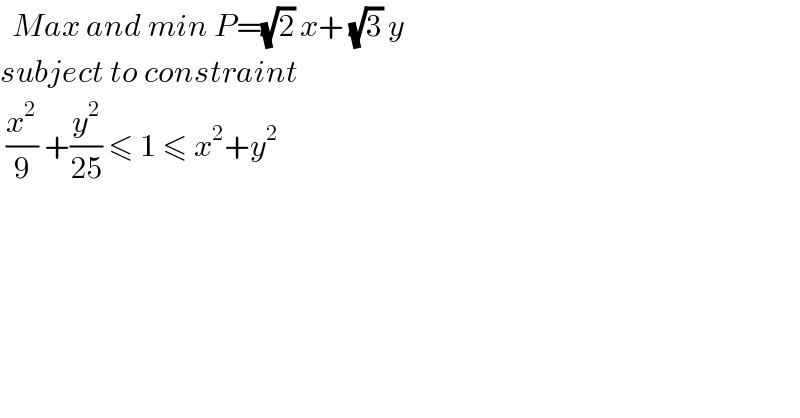
Answered by mr W last updated on 25/Jun/22

M e t h o d I

y = \frac{P - \sqrt{2} x}{\sqrt{3}}

\frac{x^{2}}{9} + \frac{1}{25} {(\frac{P - \sqrt{2} x}{\sqrt{3}})}^{2} = 1

25 x^{2} + 3 (P^{2} - 2 \sqrt{2} P x + 2 x^{2}) = 9 \times 25

31 x^{2} - 6 \sqrt{2} P x + 3 P^{2} - 225 = 0

Δ = 36 \times 2 P^{2} - 4 \times 31 (3 P^{2} - 225) = 0

P^{2} = 93

P = \pm \sqrt{93}

\Rightarrow P_{m a x} = \sqrt{93}

\Rightarrow P_{m i n} = - \sqrt{93}

Commented by mr W last updated on 25/Jun/22

Commented by Tawa11 last updated on 25/Jun/22

Great sir

Answered by mr W last updated on 25/Jun/22

M e t h o d I I

\frac{x^{2}}{3^{2}} + \frac{y^{2}}{5^{2}} = 1

\Rightarrow x = 3 \cos θ, y = 5 \sin θ

P = \sqrt{2} x + \sqrt{3} y = 3 \sqrt{2} \cos θ + 5 \sqrt{3} \sin θ

P = \sqrt{{(3 \sqrt{2})}^{2} + {(5 \sqrt{3})}^{2}} (\frac{3 \sqrt{2}}{\sqrt{{(3 \sqrt{2})}^{2} + {(5 \sqrt{3})}^{2}}} \cos θ + \frac{5 \sqrt{3}}{\sqrt{{(3 \sqrt{2})}^{2} + {(5 \sqrt{3})}^{2}}} \sin θ)

P = \sqrt{93} (\frac{3 \sqrt{2}}{\sqrt{93}} \cos θ + \frac{5 \sqrt{3}}{\sqrt{93}} \sin θ)

P = \sqrt{93} \sin (θ + \tan^{- 1} \frac{3 \sqrt{2}}{5 \sqrt{3}})

\Rightarrow P_{m a x} = \sqrt{93} a t θ = \frac{π}{2} - \tan^{- 1} \frac{3 \sqrt{2}}{5 \sqrt{3}}

\Rightarrow P_{m i n} = - \sqrt{93} a t θ = - \frac{π}{2} - \tan^{- 1} \frac{3 \sqrt{2}}{5 \sqrt{3}}

Commented by mr W last updated on 25/Jun/22

Facebook Tweet Pin