Question Number 103828 by ~blr237~ last updated on 17/Jul/20
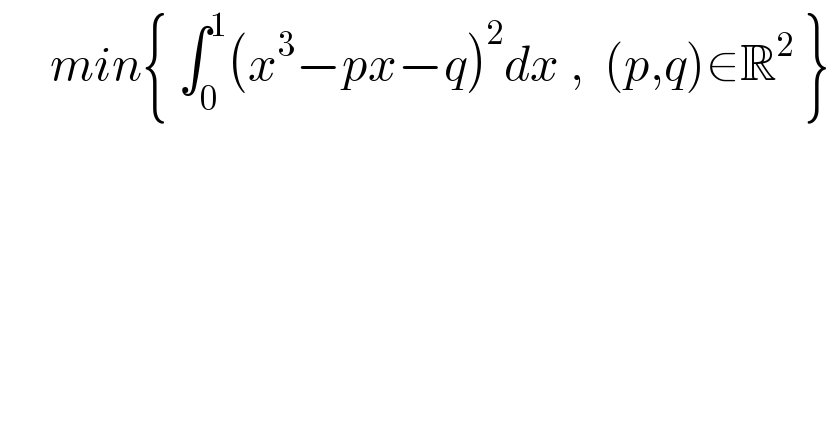
$$\:\:\:\:\:{min}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{3}} −{px}−{q}\right)^{\mathrm{2}} {dx}\:,\:\:\left({p},{q}\right)\in\mathbb{R}^{\mathrm{2}} \:\right\} \\ $$
Answered by bobhans last updated on 17/Jul/20
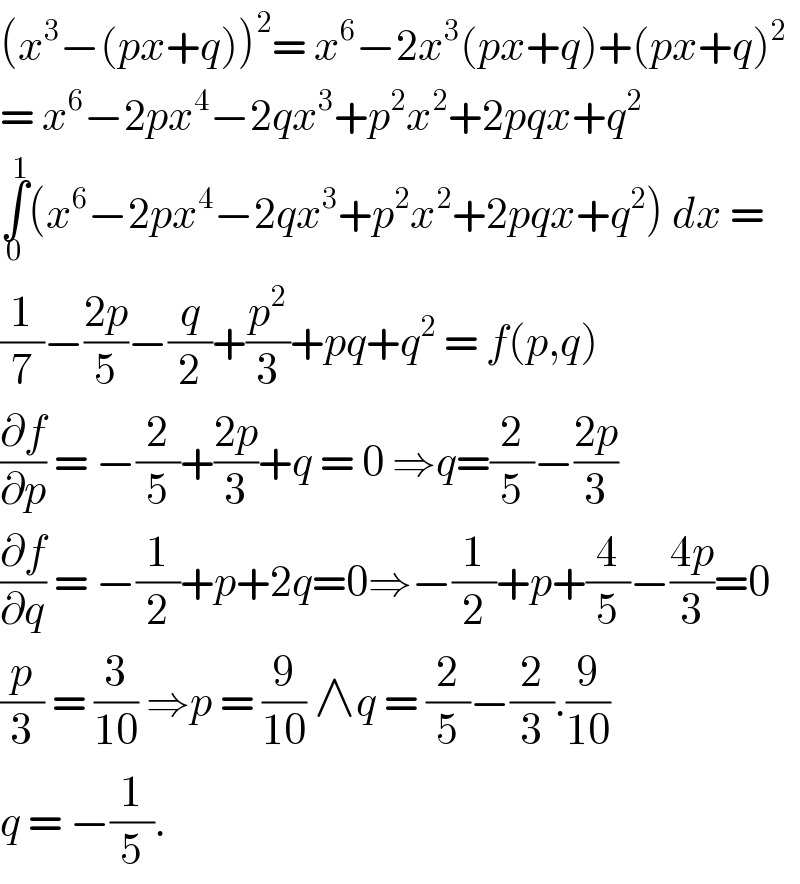
$$\left({x}^{\mathrm{3}} −\left({px}+{q}\right)\right)^{\mathrm{2}} =\:{x}^{\mathrm{6}} −\mathrm{2}{x}^{\mathrm{3}} \left({px}+{q}\right)+\left({px}+{q}\right)^{\mathrm{2}} \\ $$$$=\:{x}^{\mathrm{6}} −\mathrm{2}{px}^{\mathrm{4}} −\mathrm{2}{qx}^{\mathrm{3}} +{p}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{pqx}+{q}^{\mathrm{2}} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{6}} −\mathrm{2}{px}^{\mathrm{4}} −\mathrm{2}{qx}^{\mathrm{3}} +{p}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{pqx}+{q}^{\mathrm{2}} \right)\:{dx}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{2}{p}}{\mathrm{5}}−\frac{{q}}{\mathrm{2}}+\frac{{p}^{\mathrm{2}} }{\mathrm{3}}+{pq}+{q}^{\mathrm{2}} \:=\:{f}\left({p},{q}\right) \\ $$$$\frac{\partial{f}}{\partial{p}}\:=\:−\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{2}{p}}{\mathrm{3}}+{q}\:=\:\mathrm{0}\:\Rightarrow{q}=\frac{\mathrm{2}}{\mathrm{5}}−\frac{\mathrm{2}{p}}{\mathrm{3}} \\ $$$$\frac{\partial{f}}{\partial{q}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}+{p}+\mathrm{2}{q}=\mathrm{0}\Rightarrow−\frac{\mathrm{1}}{\mathrm{2}}+{p}+\frac{\mathrm{4}}{\mathrm{5}}−\frac{\mathrm{4}{p}}{\mathrm{3}}=\mathrm{0} \\ $$$$\frac{{p}}{\mathrm{3}}\:=\:\frac{\mathrm{3}}{\mathrm{10}}\:\Rightarrow{p}\:=\:\frac{\mathrm{9}}{\mathrm{10}}\:\wedge{q}\:=\:\frac{\mathrm{2}}{\mathrm{5}}−\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{9}}{\mathrm{10}} \\ $$$${q}\:=\:−\frac{\mathrm{1}}{\mathrm{5}}.\: \\ $$
