Menu Close

min-y-9-sin-2-x-4-csc-2-x-3-

Tinku Tara 0 Comments
Pin




Question Number 172613 by cortano1 last updated on 29/Jun/22
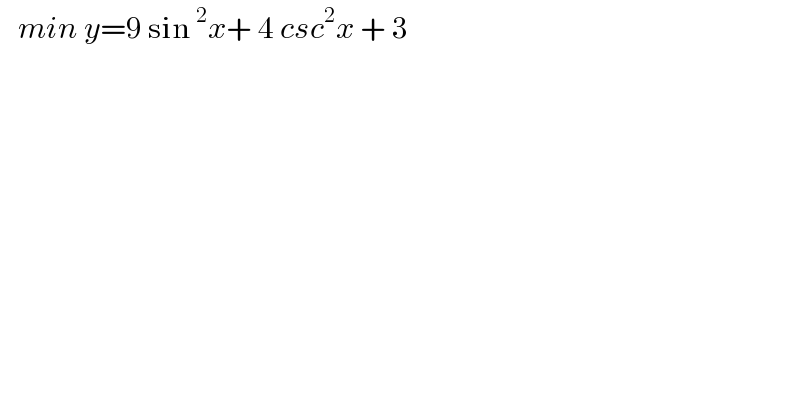
min y=9 sin^2 x+ 4 csc^2 x + 3
$$\:\:\:{min}\:{y}=\mathrm{9}\:\mathrm{sin}\:^{\mathrm{2}} {x}+\:\mathrm{4}\:{csc}^{\mathrm{2}} {x}\:+\:\mathrm{3} \\ $$
Answered by Rasheed.Sindhi last updated on 29/Jun/22
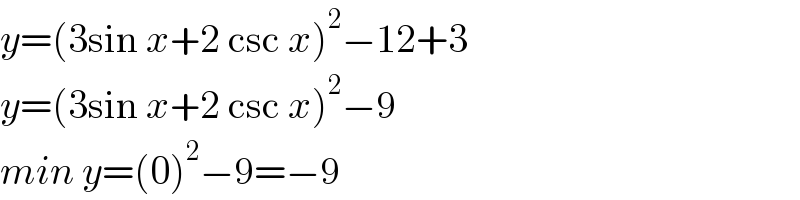
y=(3sin x+2 csc x)^2 −12+3 y=(3sin x+2 csc x)^2 −9 min y=(0)^2 −9=−9
$${y}=\left(\mathrm{3sin}\:{x}+\mathrm{2}\:\mathrm{csc}\:{x}\right)^{\mathrm{2}} −\mathrm{12}+\mathrm{3} \\ $$$${y}=\left(\mathrm{3sin}\:{x}+\mathrm{2}\:\mathrm{csc}\:{x}\right)^{\mathrm{2}} −\mathrm{9} \\ $$$${min}\:{y}=\left(\mathrm{0}\right)^{\mathrm{2}} −\mathrm{9}=−\mathrm{9} \\ $$
Commented by cortano1 last updated on 29/Jun/22
yes....min = 15
$${yes}….{min}\:=\:\mathrm{15} \\ $$
Commented by mr W last updated on 29/Jun/22
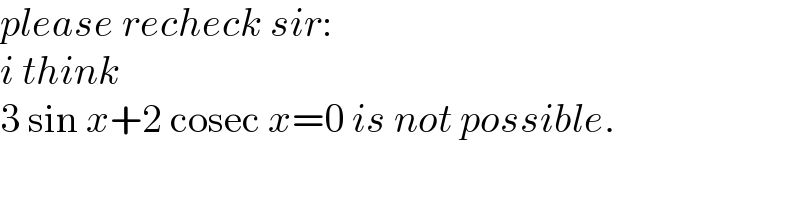
please recheck sir: i think 3 sin x+2 cosec x=0 is not possible.
$${please}\:{recheck}\:{sir}: \\ $$$${i}\:{think} \\ $$$$\mathrm{3}\:\mathrm{sin}\:{x}+\mathrm{2}\:\mathrm{cosec}\:{x}=\mathrm{0}\:{is}\:{not}\:{possible}. \\ $$
Commented by Rasheed.Sindhi last updated on 29/Jun/22
You′re right sir!
$${You}'{re}\:{right}\:\boldsymbol{{sir}}! \\ $$
Answered by mr W last updated on 29/Jun/22
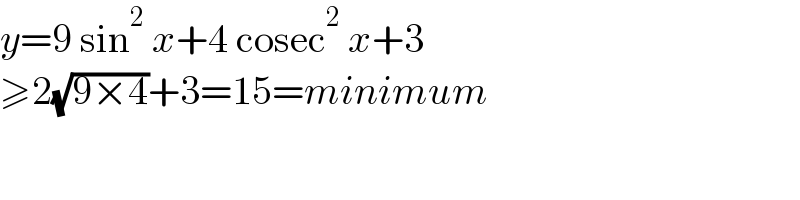
y=9 sin^2 x+4 cosec^2 x+3 ≥2(√(9×4))+3=15=minimum
$${y}=\mathrm{9}\:\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{4}\:\mathrm{cosec}^{\mathrm{2}} \:{x}+\mathrm{3} \\ $$$$\geqslant\mathrm{2}\sqrt{\mathrm{9}×\mathrm{4}}+\mathrm{3}=\mathrm{15}={minimum} \\ $$
Answered by greougoury555 last updated on 29/Jun/22
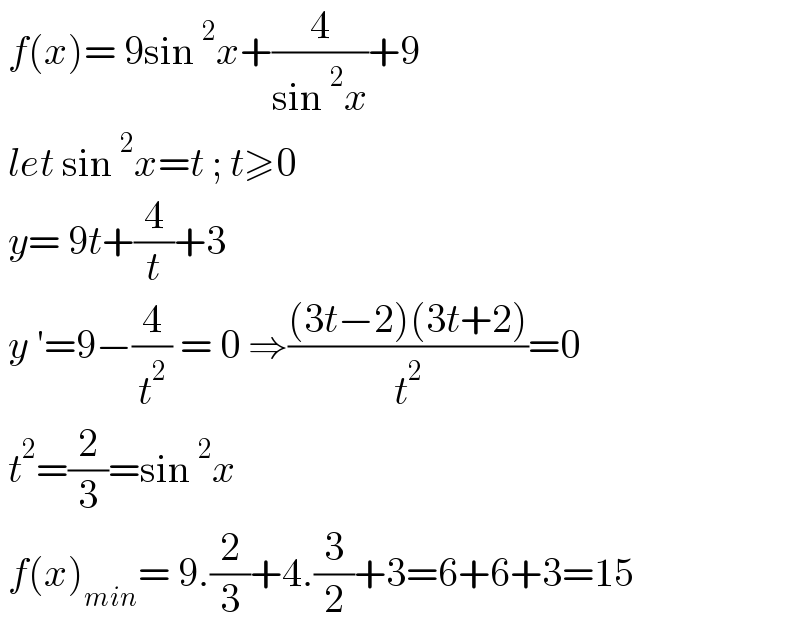
f(x)= 9sin^2 x+(4/(sin^2 x))+9 let sin^2 x=t ; t≥0 y= 9t+(4/t)+3 y ′=9−(4/t^2 ) = 0 ⇒(((3t−2)(3t+2))/t^2 )=0 t^2 =(2/3)=sin^2 x f(x)_(min) = 9.(2/3)+4.(3/2)+3=6+6+3=15
$$\:{f}\left({x}\right)=\:\mathrm{9sin}\:^{\mathrm{2}} {x}+\frac{\mathrm{4}}{\mathrm{sin}\:^{\mathrm{2}} {x}}+\mathrm{9} \\ $$$$\:{let}\:\mathrm{sin}\:^{\mathrm{2}} {x}={t}\:;\:{t}\geqslant\mathrm{0} \\ $$$$\:{y}=\:\mathrm{9}{t}+\frac{\mathrm{4}}{{t}}+\mathrm{3} \\ $$$$\:{y}\:'=\mathrm{9}−\frac{\mathrm{4}}{{t}^{\mathrm{2}} }\:=\:\mathrm{0}\:\Rightarrow\frac{\left(\mathrm{3}{t}−\mathrm{2}\right)\left(\mathrm{3}{t}+\mathrm{2}\right)}{{t}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\:{t}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$$\:{f}\left({x}\right)_{{min}} =\:\mathrm{9}.\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{4}.\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{3}=\mathrm{6}+\mathrm{6}+\mathrm{3}=\mathrm{15} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *