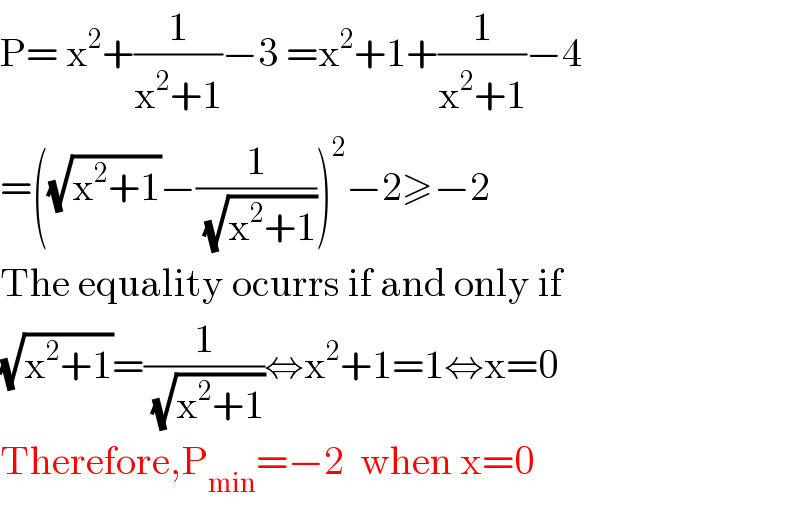Menu Close

Minimum-value-of-x-2-1-x-2-1-3-is-

Tinku Tara 0 Comments
Pin




Question Number 112624 by Aina Samuel Temidayo last updated on 09/Sep/20
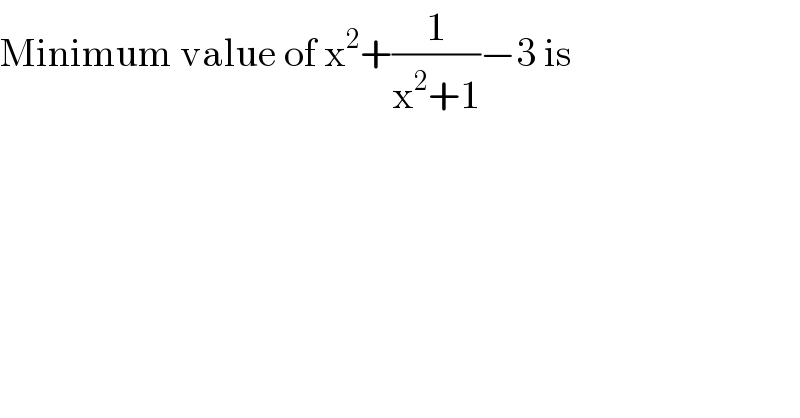
Minimum value of x^2 +(1/(x^2 +1))−3 is
$$\mathrm{Minimum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{3}\:\mathrm{is} \\ $$
Answered by MJS_new last updated on 09/Sep/20
x^2 +1+(1/(x^2 +1))−4 x^2 +1=t≥1 t+(1/t)−4 (d/dt)[t+(1/t)−4]=1−(1/t^2 )=0 ⇒ t=1 ⇒ x^2 +1=1 ⇒ x=0 ⇒ answer is −2
$${x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{4} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}={t}\geqslant\mathrm{1} \\ $$$${t}+\frac{\mathrm{1}}{{t}}−\mathrm{4} \\ $$$$\frac{{d}}{{dt}}\left[{t}+\frac{\mathrm{1}}{{t}}−\mathrm{4}\right]=\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }=\mathrm{0}\:\Rightarrow\:{t}=\mathrm{1}\:\Rightarrow\:{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{1}\:\Rightarrow\:{x}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:−\mathrm{2} \\ $$
Answered by ajfour last updated on 09/Sep/20
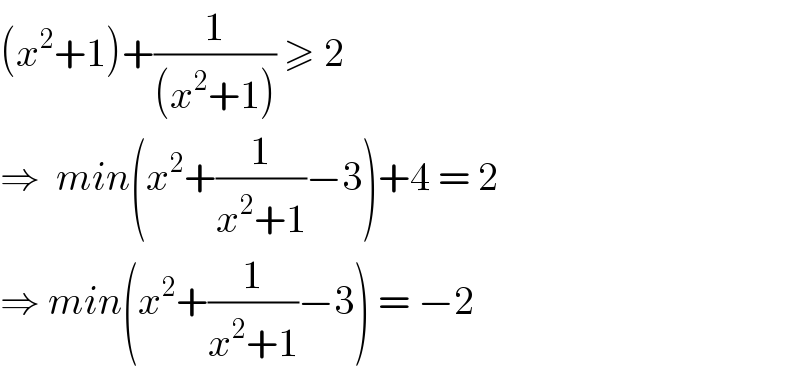
(x^2 +1)+(1/((x^2 +1))) ≥ 2 ⇒ min(x^2 +(1/(x^2 +1))−3)+4 = 2 ⇒ min(x^2 +(1/(x^2 +1))−3) = −2
$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:\geqslant\:\mathrm{2} \\ $$$$\Rightarrow\:\:{min}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{3}\right)+\mathrm{4}\:=\:\mathrm{2} \\ $$$$\Rightarrow\:{min}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{3}\right)\:=\:−\mathrm{2} \\ $$
Commented by Aina Samuel Temidayo last updated on 09/Sep/20
Thanks.
$$\mathrm{Thanks}. \\ $$
Answered by 1549442205PVT last updated on 09/Sep/20
P= x^2 +(1/(x^2 +1))−3 =x^2 +1+(1/(x^2 +1))−4 =((√(x^2 +1))−(1/( (√(x^2 +1)))))^2 −2≥−2 The equality ocurrs if and only if (√(x^2 +1))=(1/( (√(x^2 +1))))⇔x^2 +1=1⇔x=0 Therefore,P_(min) =−2 when x=0
$$\mathrm{P}=\:\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{3}\:=\mathrm{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{4} \\ $$$$=\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\right)^{\mathrm{2}} −\mathrm{2}\geqslant−\mathrm{2} \\ $$$$\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$$$\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{1}\Leftrightarrow\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{Therefore},\mathrm{P}_{\mathrm{min}} =−\mathrm{2}\:\:\mathrm{when}\:\mathrm{x}=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *