Question Number 14364 by RasheedSindhi last updated on 31/May/17

$$\mathrm{Modification}\:\mathrm{of}\:\mathrm{Q}#\mathrm{14157} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{xy}=\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} −\mathrm{yz}=\mathrm{b}^{\mathrm{2}} \\ $$$$\mathrm{z}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{zx}=\mathrm{c}^{\mathrm{2}} \\ $$$$\mathrm{Pl}\:\mathrm{discuss}\:\mathrm{also}\:\mathrm{geometrical}/ \\ $$$$\mathrm{trigonometrical}\:\mathrm{aspects}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
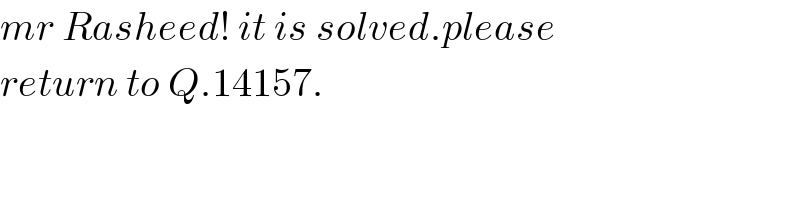
$${mr}\:{Rasheed}!\:{it}\:{is}\:{solved}.{please}\: \\ $$$${return}\:{to}\:{Q}.\mathrm{14157}. \\ $$
Commented by RasheedSindhi last updated on 31/May/17

$$\mathrm{Mr}/\mathrm{Miss}\:\mathrm{behi}.\mathrm{This}\:\mathrm{is}\:\mathrm{somewhat} \\ $$$$\mathrm{different}\:\mathrm{from}\:\mathrm{Q}#\mathrm{14157}.\mathrm{Here} \\ $$$$\mathrm{you}\:\mathrm{can}'\mathrm{t}\:\mathrm{draw}\:\mathrm{such}\:\mathrm{triangle} \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{did}\:\mathrm{in}\:\mathrm{answer}\:\mathrm{of}\:\mathrm{mentioned} \\ $$$$\mathrm{question}.\mathrm{Pl}\:\mathrm{try}\:\mathrm{such}\:\mathrm{geometrical} \\ $$$$\mathrm{solution}\:\mathrm{here}\:\mathrm{as}\:\mathrm{you}\:\mathrm{did}\:\mathrm{before}. \\ $$
Commented by mrW1 last updated on 31/May/17
Commented by mrW1 last updated on 31/May/17

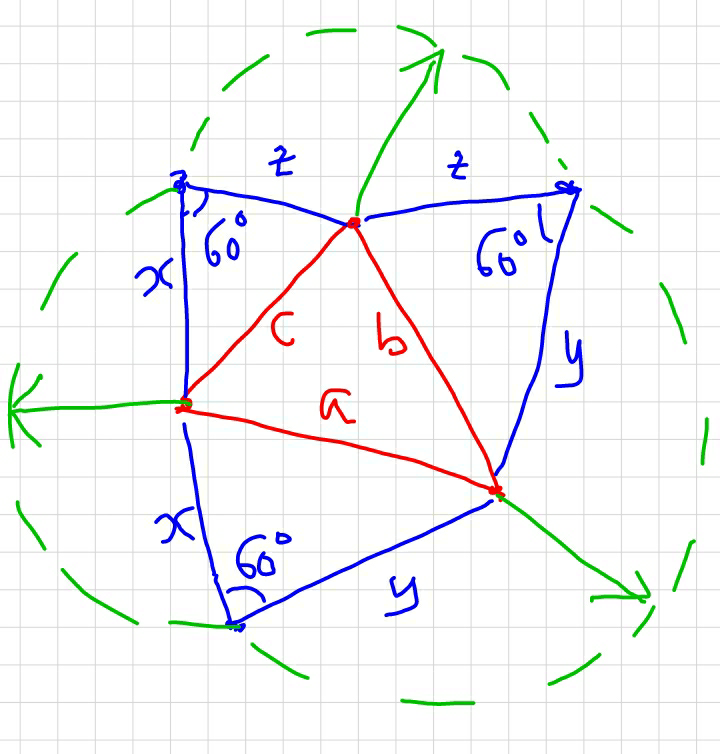
$${This}\:{is}\:{the}\:{geometrical}\:{interpretation} \\ $$$${of}\:{the}\:{solution}. \\ $$
Commented by RasheedSindhi last updated on 31/May/17

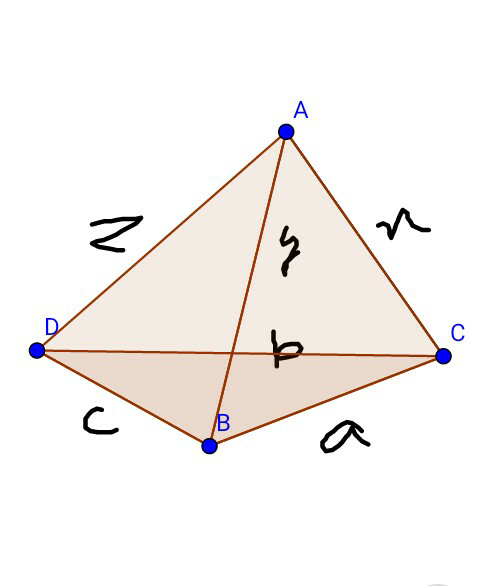
$$\mathrm{Fine}\:\mathrm{idea}!\:\mathrm{Very}\:\mathrm{general}\:\mathrm{also}!\:\mathrm{It} \\ $$$$\mathrm{is}\:\mathrm{for}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{kxy}=\mathrm{a}^{\mathrm{2}} \:\mathrm{for}\:\mathrm{any} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{k}.\:\mathrm{My}\:\mathrm{idea}\:\mathrm{is}\:\mathrm{also} \\ $$$$\mathrm{general}\:\mathrm{but}\:\mathrm{it}\:\mathrm{needs}\:\mathrm{space}.\: \\ $$$$\mathrm{See}\:\mathrm{image}\:\mathrm{below} \\ $$$$\mathrm{At}\:\mathrm{A}\:\mathrm{all}\:\mathrm{the}\:\mathrm{triangular}\:\mathrm{faces} \\ $$$$\mathrm{have}\:\mathrm{equal}\:\mathrm{angles}\:\mathrm{each}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\mathrm{60}°. \\ $$
Commented by RasheedSindhi last updated on 31/May/17
Commented by mrW1 last updated on 31/May/17

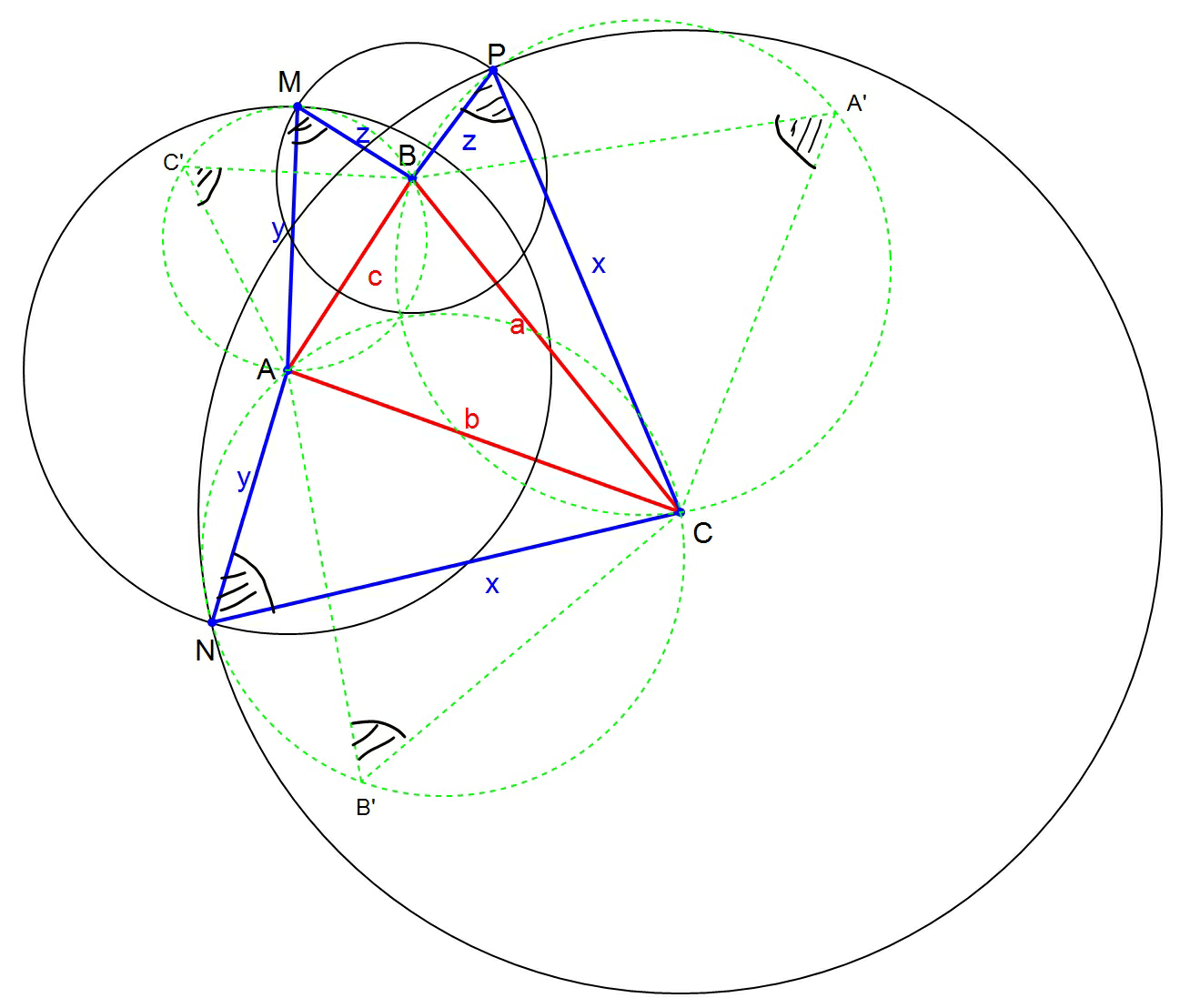
$${Your}\:{idea}\:{with}\:{the}\:{pyramid}\:{is}\:{remarkable}! \\ $$$$ \\ $$$${I}\:{thought}\:{in}\:{plane}.\:{But}\:{the}\:{geometrical} \\ $$$${meaning}\:{from}\:{us}\:{is}\:{the}\:{same}.\:{If}\:{you} \\ $$$${fold}\:{my}\:{figure}\:{at}\:{the}\:{lines}\:{a},{b},{c},\:{you} \\ $$$${will}\:{get}\:{the}\:{same}\:{pyramid}\:{as}\:{yours}.\:{Or} \\ $$$${if}\:{you}\:{unfold}\:{your}\:{pyramid},\:{you}\:{will} \\ $$$${get}\:{the}\:{same}\:{figure}\:{as}\:{mines}. \\ $$$$ \\ $$$${I}\:{put}\:{a}\:{more}\:{detailed}\:{figure}. \\ $$
Commented by mrW1 last updated on 31/May/17
Commented by RasheedSindhi last updated on 01/Jun/17

$$\mathcal{B}{elieve}\:{me}\:{sir},\:\mathcal{I}\:{also}\:{discovered} \\ $$$${same}\:{connection}\:{after}\:{my}\:{post}! \\ $$$${Anyway}\:{both}\:{are}\:{same}! \\ $$$${The}\:{idea}\:{came}\:{into}\:{my}\:{mind} \\ $$$${in}\:{this}\:{way}:{Three}\:{line}\:{segments} \\ $$$${x},{y}\:\&{z}\:{with}\:{common}\:{endpoint} \\ $$$${can}\:{be}\:{drawn}\:{at}\:\mathrm{120}°\:{in}\:{a}\:{plane}. \\ $$$${Now}\:{angles}\:{should}\:{be}\:{decreased} \\ $$$${to}\:\mathrm{60}°.{This}\:{can}\:{be}\:{done}\:{by}\:{lifting} \\ $$$${up}\left({or}\:{below}\right)\:{non}-{common} \\ $$$${endpoints}.\:{S}\mathrm{o}\:{in}\:{this}\:{way}\:{the} \\ $$$${the}\:{idea}\:{of}\:{pyramid}\:{came}\:{in}\:{mind}. \\ $$
