Question Number 160526 by mathocean1 last updated on 14/Dec/21
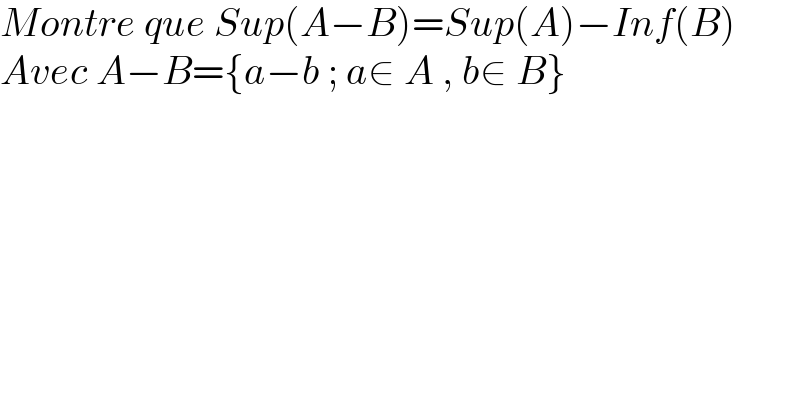
$${Montre}\:{que}\:{Sup}\left({A}−{B}\right)={Sup}\left({A}\right)−{Inf}\left({B}\right) \\ $$$${Avec}\:{A}−{B}=\left\{{a}−{b}\:;\:{a}\in\:{A}\:,\:{b}\in\:{B}\right\} \\ $$
Answered by puissant last updated on 01/Dec/21
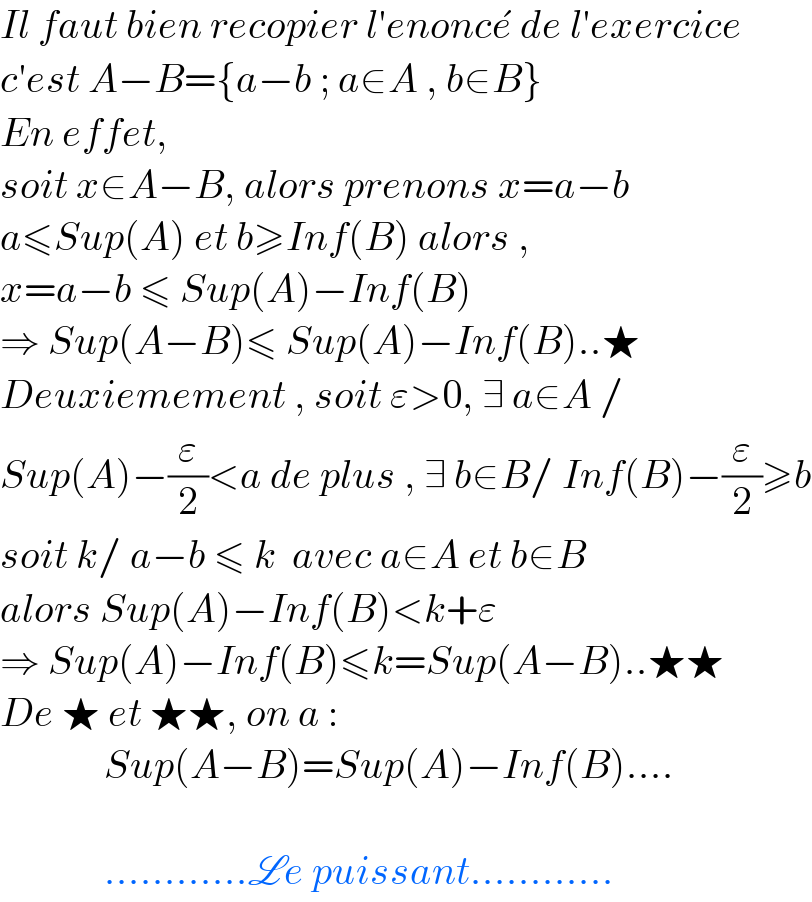
$${Il}\:{faut}\:{bien}\:{recopier}\:{l}'{enonc}\acute {{e}}\:{de}\:{l}'{exercice} \\ $$$${c}'{est}\:{A}−{B}=\left\{{a}−{b}\:;\:{a}\in{A}\:,\:{b}\in{B}\right\} \\ $$$${En}\:{effet}, \\ $$$${soit}\:{x}\in{A}−{B},\:{alors}\:{prenons}\:{x}={a}−{b} \\ $$$${a}\leqslant{Sup}\left({A}\right)\:{et}\:{b}\geqslant{Inf}\left({B}\right)\:{alors}\:, \\ $$$${x}={a}−{b}\:\leqslant\:{Sup}\left({A}\right)−{Inf}\left({B}\right) \\ $$$$\Rightarrow\:{Sup}\left({A}−{B}\right)\leqslant\:{Sup}\left({A}\right)−{Inf}\left({B}\right)..\bigstar \\ $$$${Deuxiemement}\:,\:{soit}\:\varepsilon>\mathrm{0},\:\exists\:{a}\in{A}\:/ \\ $$$${Sup}\left({A}\right)−\frac{\varepsilon}{\mathrm{2}}<{a}\:{de}\:{plus}\:,\:\exists\:{b}\in{B}/\:{Inf}\left({B}\right)−\frac{\varepsilon}{\mathrm{2}}\geqslant{b} \\ $$$${soit}\:{k}/\:{a}−{b}\:\leqslant\:{k}\:\:{avec}\:{a}\in{A}\:{et}\:{b}\in{B} \\ $$$${alors}\:{Sup}\left({A}\right)−{Inf}\left({B}\right)<{k}+\varepsilon \\ $$$$\Rightarrow\:{Sup}\left({A}\right)−{Inf}\left({B}\right)\leqslant{k}={Sup}\left({A}−{B}\right)..\bigstar\bigstar \\ $$$${De}\:\bigstar\:{et}\:\bigstar\bigstar,\:{on}\:{a}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{Sup}\left({A}−{B}\right)={Sup}\left({A}\right)−{Inf}\left({B}\right)…. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:…………\mathscr{L}{e}\:{puissant}………… \\ $$
Commented by mathocean1 last updated on 14/Dec/21

$${Thank}\:{you}. \\ $$$${corrected}. \\ $$
