Question Number 158794 by SANOGO last updated on 08/Nov/21
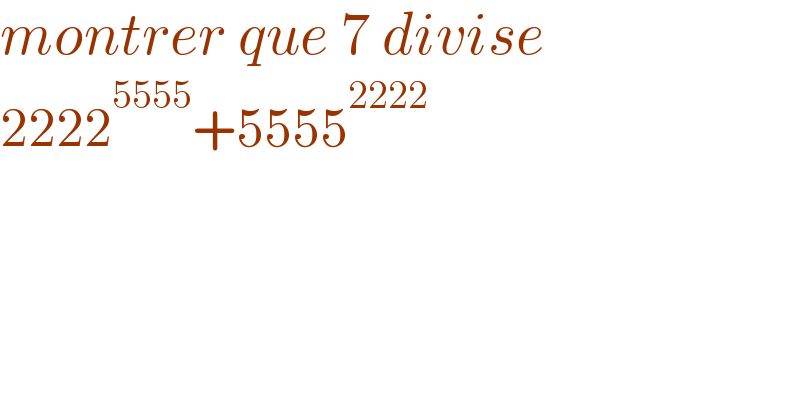
$${montrer}\:{que}\:\mathrm{7}\:{divise} \\ $$$$\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 09/Nov/21

$${We}'{ll}\:\:{determine}\:{remainders} \\ $$$${of}\:\mathrm{2222}^{\mathrm{5555}} \:\&\:\mathrm{5555}^{\mathrm{2222}} \:{separately} \\ $$$${and}\:{then}\:{add}\:{them}: \\ $$$$\blacktriangleright\mathrm{2222}^{\mathrm{5555}} \equiv{x}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\:\mathrm{2222}\equiv\mathrm{3}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\:\mathrm{2222}^{\mathrm{5}} \equiv\mathrm{3}^{\mathrm{5}} \equiv\mathrm{5}\left({mod}\:\mathrm{7}\right)……….\left({i}\right) \\ $$$$\because\mathrm{gcd}\left(\mathrm{2222},\mathrm{7}\right)=\mathrm{1}\:\&\:\phi\left(\mathrm{7}\right)=\mathrm{6} \\ $$$$\therefore\mathrm{2222}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\left(\mathrm{2222}^{\mathrm{6}} \right)^{\mathrm{925}} \equiv\left(\mathrm{1}\right)^{\mathrm{925}} \left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\mathrm{2222}^{\mathrm{5550}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right)…………\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\:\:\:\:\mathrm{2222}^{\mathrm{5}} .\mathrm{2222}^{\mathrm{5550}} \equiv\mathrm{5}.\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\mathrm{2222}^{\mathrm{5555}} \equiv\mathrm{5}\left({mod}\:\mathrm{7}\right)………….{A} \\ $$$$\blacktriangleright\mathrm{5555}^{\mathrm{2222}} \equiv{y}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\mathrm{gcd}\left(\mathrm{5555},\mathrm{7}\right)=\mathrm{1}\:\&\:\phi\left(\mathrm{7}\right)=\mathrm{6} \\ $$$$\:\:\:\:\mathrm{5555}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\left(\mathrm{5555}^{\mathrm{6}} \right)^{\mathrm{370}} \equiv\left(\mathrm{1}\right)^{\mathrm{370}} \left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\mathrm{5555}^{\mathrm{2220}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right)……..\left({iii}\right) \\ $$$$\:\:\:\:\mathrm{5555}\equiv\mathrm{4}\left({mod}\:\mathrm{7}\right) \\ $$$$\:\:\:\:\mathrm{5555}^{\mathrm{2}} \equiv\mathrm{4}^{\mathrm{2}} \equiv\mathrm{2}\left({mod}\:\mathrm{7}\right)……..\left({iv}\right) \\ $$$$\left({iii}\right)×\left({iv}\right): \\ $$$$\:\:\:\:\mathrm{5555}^{\mathrm{2222}} \equiv\mathrm{2}\left({mod}\:\mathrm{7}\right)……………..{B} \\ $$$${A}+{B}: \\ $$$$\:\:\:\:\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \equiv\mathrm{5}+\mathrm{2}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathcal{H}{ence}\:\mathrm{7}\:{divides}\:{given}\:{expression}. \\ $$$$\:\:\overset{\preccurlyeq\underset{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} {\overset{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} {\mathrm{FORMULA}\:\mathrm{USED}\succcurlyeq}}} {\begin{array}{|c|}{\underset{{provided}\:{that}\:\mathrm{gcd}\left({a},{m}\right)=\mathrm{1}} {{a}^{\phi\left({m}\right)} \equiv\mathrm{1}\left({mod}\:{m}\right)}}\\\hline\end{array}^{} } \\ $$
Commented by SANOGO last updated on 09/Nov/21
$${merci}\:{bien} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Nov/21
![MOD 7 2222^(5555) +5555^(2222) =2222^(6×925+5) +5555^(6×370+2) [∵φ(7)=6] =(2222^6 )^(925) .2222^5 +(5555^6 )^(370) .5555^2 =(1^(925) )(2222^5 +(1^(370) )(5555^2 ) [ ∵2222^6 ≡1 & 5555^6 ≡1(mod 7)] =2222^5 +5555^2 =3^5 +4^2 [∵2222≡3 & 5555≡4 (mod 7)] =5+2=7=0 Hence 7 ∣ (2222^(5555) +5555^(2222) )](https://www.tinkutara.com/question/Q158836.png)
$$\:\:\:\:\:\:\mathrm{MOD}\:\mathrm{7} \\ $$$$\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \\ $$$$=\mathrm{2222}^{\mathrm{6}×\mathrm{925}+\mathrm{5}} +\mathrm{5555}^{\mathrm{6}×\mathrm{370}+\mathrm{2}} \left[\because\phi\left(\mathrm{7}\right)=\mathrm{6}\right] \\ $$$$=\left(\mathrm{2222}^{\mathrm{6}} \right)^{\mathrm{925}} .\mathrm{2222}^{\mathrm{5}} +\left(\mathrm{5555}^{\mathrm{6}} \right)^{\mathrm{370}} .\mathrm{5555}^{\mathrm{2}} \\ $$$$=\left(\mathrm{1}^{\mathrm{925}} \right)\left(\mathrm{2222}^{\mathrm{5}} +\left(\mathrm{1}^{\mathrm{370}} \right)\left(\mathrm{5555}^{\mathrm{2}} \right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\left[\:\because\mathrm{2222}^{\mathrm{6}} \equiv\mathrm{1}\:\&\:\mathrm{5555}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right)\right] \\ $$$$=\mathrm{2222}^{\mathrm{5}} +\mathrm{5555}^{\mathrm{2}} \\ $$$$=\mathrm{3}^{\mathrm{5}} +\mathrm{4}^{\mathrm{2}} \:\left[\because\mathrm{2222}\equiv\mathrm{3}\:\&\:\mathrm{5555}\equiv\mathrm{4}\:\left({mod}\:\mathrm{7}\right)\right] \\ $$$$=\mathrm{5}+\mathrm{2}=\mathrm{7}=\mathrm{0} \\ $$$${Hence}\: \\ $$$$\:\:\:\:\:\:\mathrm{7}\:\mid\:\left(\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \right) \\ $$
Commented by SANOGO last updated on 10/Nov/21
$${merci}\:{bien} \\ $$
Commented by SANOGO last updated on 10/Nov/21
$${merci}\:{bien} \\ $$
