Question Number 168628 by SANOGO last updated on 14/Apr/22
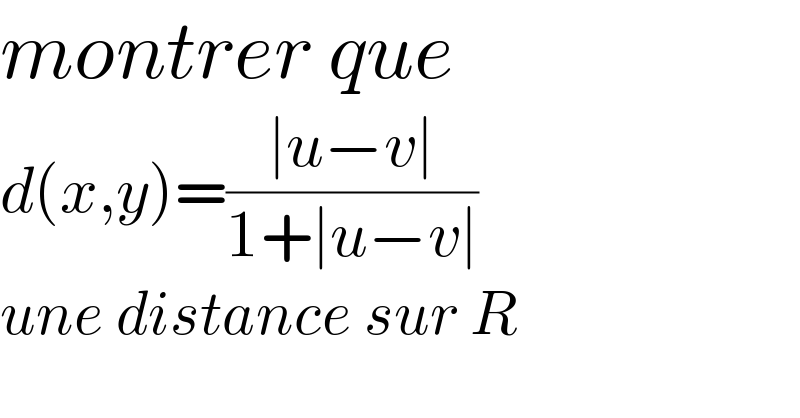
$${montrer}\:{que} \\ $$$${d}\left({x},{y}\right)=\frac{\mid{u}−{v}\mid}{\mathrm{1}+\mid{u}−{v}\mid}\: \\ $$$${une}\:{distance}\:{sur}\:{R} \\ $$
Answered by ArielVyny last updated on 15/Apr/22
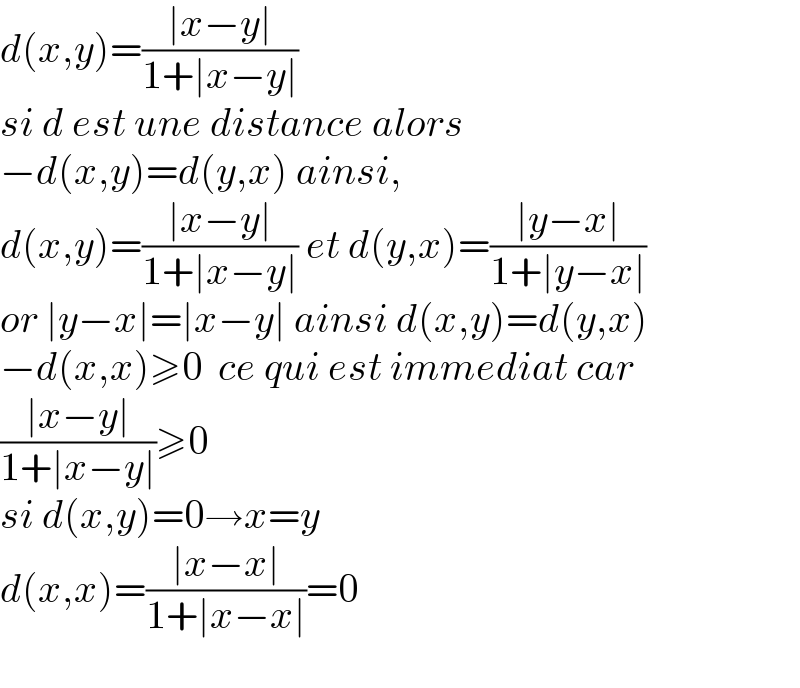
$${d}\left({x},{y}\right)=\frac{\mid{x}−{y}\mid}{\mathrm{1}+\mid{x}−{y}\mid} \\ $$$${si}\:{d}\:{est}\:{une}\:{distance}\:{alors} \\ $$$$−{d}\left({x},{y}\right)={d}\left({y},{x}\right)\:{ainsi}, \\ $$$${d}\left({x},{y}\right)=\frac{\mid{x}−{y}\mid}{\mathrm{1}+\mid{x}−{y}\mid}\:{et}\:{d}\left({y},{x}\right)=\frac{\mid{y}−{x}\mid}{\mathrm{1}+\mid{y}−{x}\mid} \\ $$$${or}\:\mid{y}−{x}\mid=\mid{x}−{y}\mid\:{ainsi}\:{d}\left({x},{y}\right)={d}\left({y},{x}\right) \\ $$$$−{d}\left({x},{x}\right)\geqslant\mathrm{0}\:\:{ce}\:{qui}\:{est}\:{immediat}\:{car} \\ $$$$\frac{\mid{x}−{y}\mid}{\mathrm{1}+\mid{x}−{y}\mid}\geqslant\mathrm{0} \\ $$$${si}\:{d}\left({x},{y}\right)=\mathrm{0}\rightarrow{x}={y} \\ $$$${d}\left({x},{x}\right)=\frac{\mid{x}−{x}\mid}{\mathrm{1}+\mid{x}−{x}\mid}=\mathrm{0} \\ $$$$ \\ $$
