Montrer-que-k-0-2n-1-cos-2n-k-2n-nC-2n-n-2-2n-1-

Question Number 146924 by Willson last updated on 16/Jul/21

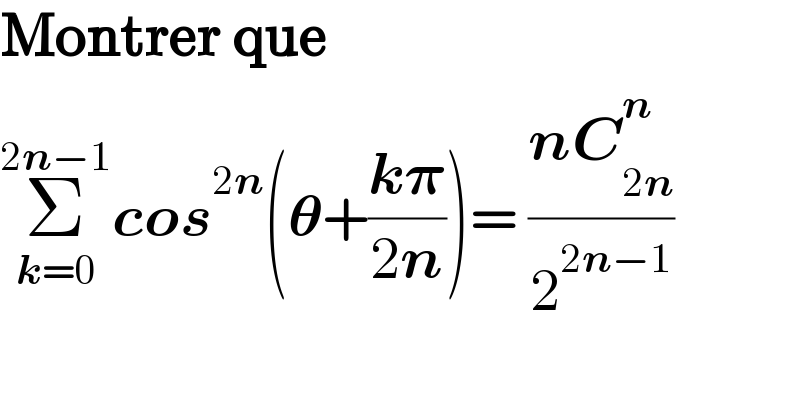
Montrer que Σ_(k=0) ^(2n−1) cos^(2n) (𝛉+((k𝛑)/(2n)))= ((nC_(2n) ^n )/2^(2n−1) )

$$\boldsymbol{\mathrm{Montrer}}\:\boldsymbol{\mathrm{que}} \\ $$$$\underset{\boldsymbol{{k}}=\mathrm{0}} {\overset{\mathrm{2}\boldsymbol{{n}}−\mathrm{1}} {\sum}}\boldsymbol{{cos}}^{\mathrm{2}\boldsymbol{{n}}} \left(\boldsymbol{\theta}+\frac{\boldsymbol{{k}\pi}}{\mathrm{2}\boldsymbol{{n}}}\right)=\:\frac{\boldsymbol{{nC}}_{\mathrm{2}\boldsymbol{{n}}} ^{\boldsymbol{{n}}} }{\mathrm{2}^{\mathrm{2}\boldsymbol{{n}}−\mathrm{1}} } \\ $$

Answered by mindispower last updated on 17/Jul/21

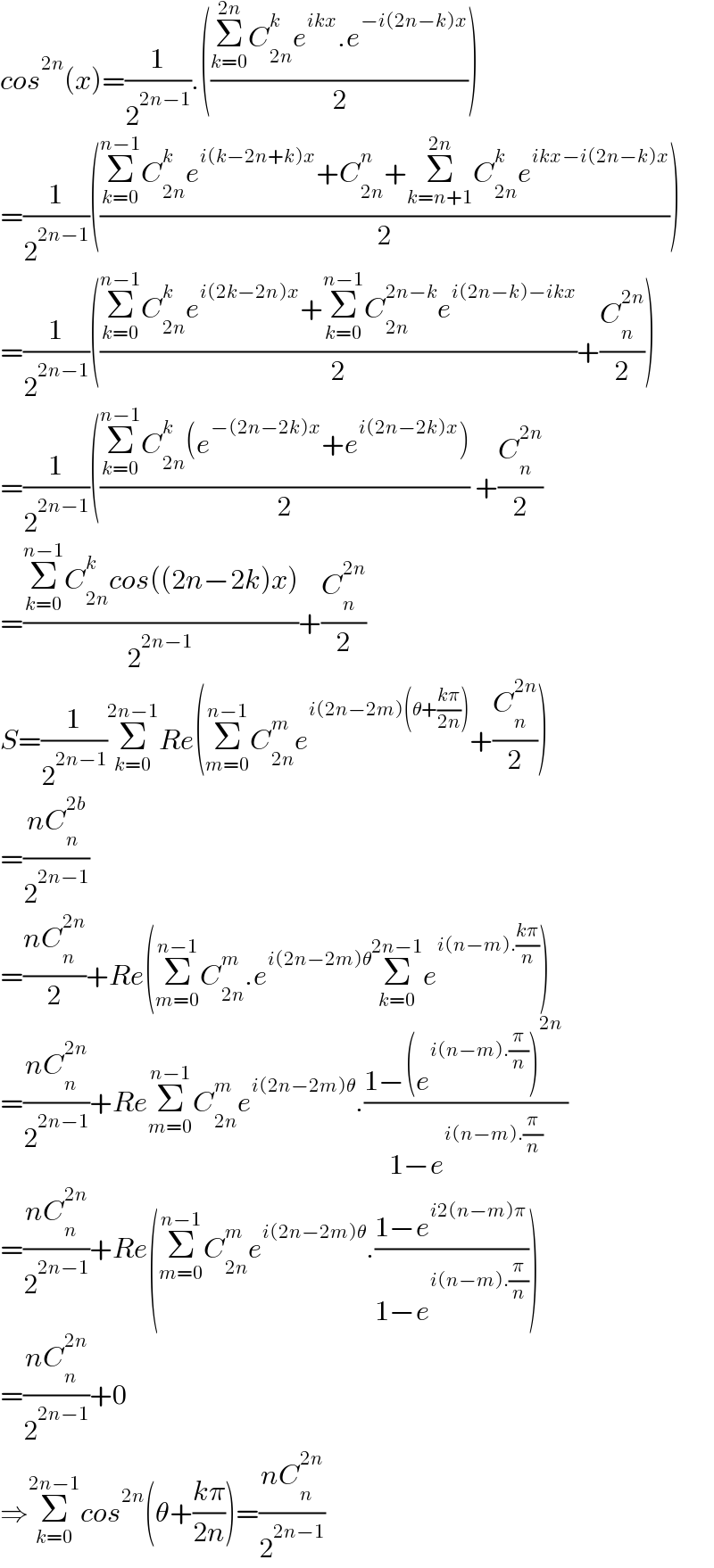
cos^(2n) (x)=(1/2^(2n−1) ).(((Σ_(k=0) ^(2n) C_(2n) ^k e^(ikx) .e^(−i(2n−k)x) )/2)) =(1/2^(2n−1) )(((Σ_(k=0) ^(n−1) C_(2n) ^k e^(i(k−2n+k)x) +C_(2n) ^n +Σ_(k=n+1) ^(2n) C_(2n) ^k e^(ikx−i(2n−k)x) )/2)) =(1/2^(2n−1) )(((Σ_(k=0) ^(n−1) C_(2n) ^k e^(i(2k−2n)x) +Σ_(k=0) ^(n−1) C_(2n) ^(2n−k) e^(i(2n−k)−ikx) )/2)+(C_n ^(2n) /2)) =(1/2^(2n−1) )(((Σ_(k=0) ^(n−1) C_(2n) ^k (e^(−(2n−2k)x) +e^(i(2n−2k)x) ))/2) +(C_n ^(2n) /2) =((Σ_(k=0) ^(n−1) C_(2n) ^k cos((2n−2k)x))/2^(2n−1) )+(C_n ^(2n) /2) S=(1/2^(2n−1) )Σ_(k=0) ^(2n−1) Re(Σ_(m=0) ^(n−1) C_(2n) ^m e^(i(2n−2m)(θ+((kπ)/(2n)))) +(C_n ^(2n) /2)) =((nC_n ^(2b) )/2^(2n−1) ) =((nC_n ^(2n) )/2)+Re(Σ_(m=0) ^(n−1) C_(2n) ^m .e^(i(2n−2m)θ) Σ_(k=0) ^(2n−1) e^(i(n−m).((kπ)/n)) ) =((nC_n ^(2n) )/2^(2n−1) )+ReΣ_(m=0) ^(n−1) C_(2n) ^m e^(i(2n−2m)θ) .((1−(e^(i(n−m).(π/n)) )^(2n) )/(1−e^(i(n−m).(π/n)) )) =((nC_n ^(2n) )/2^(2n−1) )+Re(Σ_(m=0) ^(n−1) C_(2n) ^m e^(i(2n−2m)θ) .((1−e^(i2(n−m)π) )/(1−e^(i(n−m).(π/n)) ))) =((nC_n ^(2n) )/2^(2n−1) )+0 ⇒Σ_(k=0) ^(2n−1) cos^(2n) (θ+((kπ)/(2n)))=((nC_n ^(2n) )/2^(2n−1) )

$${cos}^{\mathrm{2}{n}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }.\left(\frac{\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} {e}^{{ikx}} .{e}^{−{i}\left(\mathrm{2}{n}−{k}\right){x}} }{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }\left(\frac{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} {e}^{{i}\left({k}−\mathrm{2}{n}+{k}\right){x}} +{C}_{\mathrm{2}{n}} ^{{n}} +\underset{{k}={n}+\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} {e}^{{ikx}−{i}\left(\mathrm{2}{n}−{k}\right){x}} }{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }\left(\frac{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} {e}^{{i}\left(\mathrm{2}{k}−\mathrm{2}{n}\right){x}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{\mathrm{2}{n}−{k}} {e}^{{i}\left(\mathrm{2}{n}−{k}\right)−{ikx}} }{\mathrm{2}}+\frac{{C}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }\left(\frac{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} \left({e}^{−\left(\mathrm{2}{n}−\mathrm{2}{k}\right){x}} +{e}^{{i}\left(\mathrm{2}{n}−\mathrm{2}{k}\right){x}} \right)}{\mathrm{2}}\:+\frac{{C}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}}\right. \\ $$$$=\frac{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} {cos}\left(\left(\mathrm{2}{n}−\mathrm{2}{k}\right){x}\right)}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }+\frac{{C}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}{Re}\left(\underset{{m}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{{m}} {e}^{{i}\left(\mathrm{2}{n}−\mathrm{2}{m}\right)\left(\theta+\frac{{k}\pi}{\mathrm{2}{n}}\right)} +\frac{{C}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}}\right) \\ $$$$=\frac{{nC}_{{n}} ^{\mathrm{2}{b}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} } \\ $$$$=\frac{{nC}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}}+{Re}\left(\underset{{m}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{{m}} .{e}^{{i}\left(\mathrm{2}{n}−\mathrm{2}{m}\right)\theta} \underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}{e}^{{i}\left({n}−{m}\right).\frac{{k}\pi}{{n}}} \right) \\ $$$$=\frac{{nC}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }+{Re}\underset{{m}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{{m}} {e}^{{i}\left(\mathrm{2}{n}−\mathrm{2}{m}\right)\theta} .\frac{\mathrm{1}−\left({e}^{{i}\left({n}−{m}\right).\frac{\pi}{{n}}} \right)^{\mathrm{2}{n}} \:}{\mathrm{1}−{e}^{{i}\left({n}−{m}\right).\frac{\pi}{{n}}} } \\ $$$$=\frac{{nC}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }+{Re}\left(\underset{{m}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{\mathrm{2}{n}} ^{{m}} {e}^{{i}\left(\mathrm{2}{n}−\mathrm{2}{m}\right)\theta} .\frac{\mathrm{1}−{e}^{{i}\mathrm{2}\left({n}−{m}\right)\pi} }{\mathrm{1}−{e}^{{i}\left({n}−{m}\right).\frac{\pi}{{n}}} }\right) \\ $$$$=\frac{{nC}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }+\mathrm{0} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}{cos}^{\mathrm{2}{n}} \left(\theta+\frac{{k}\pi}{\mathrm{2}{n}}\right)=\frac{{nC}_{{n}} ^{\mathrm{2}{n}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} } \\ $$

Facebook Tweet Pin

Montrer-que-k-0-2n-1-cos-2n-k-2n-nC-2n-n-2-2n-1-

Leave a Reply Cancel reply