Question Number 171608 by SANOGO last updated on 18/Jun/22
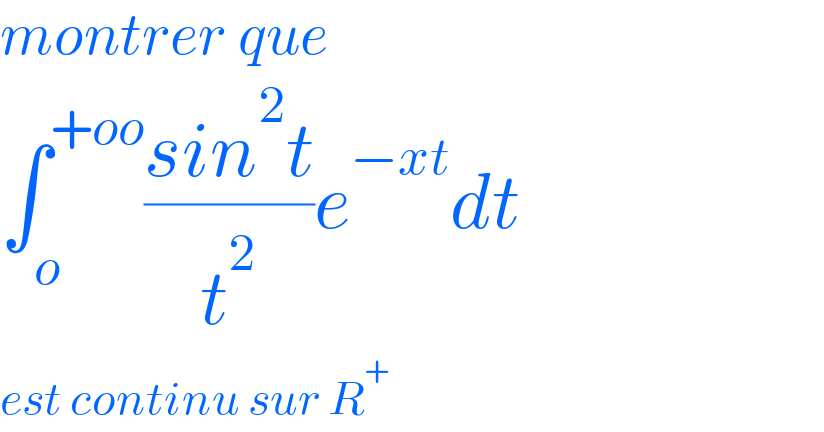
$${montrer}\:{que} \\ $$$$\int_{{o}} ^{+{oo}} \frac{{sin}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} }{e}^{−{xt}} {dt} \\ $$$${est}\:{continu}\:{sur}\:{R}^{+} \\ $$
Answered by aleks041103 last updated on 18/Jun/22
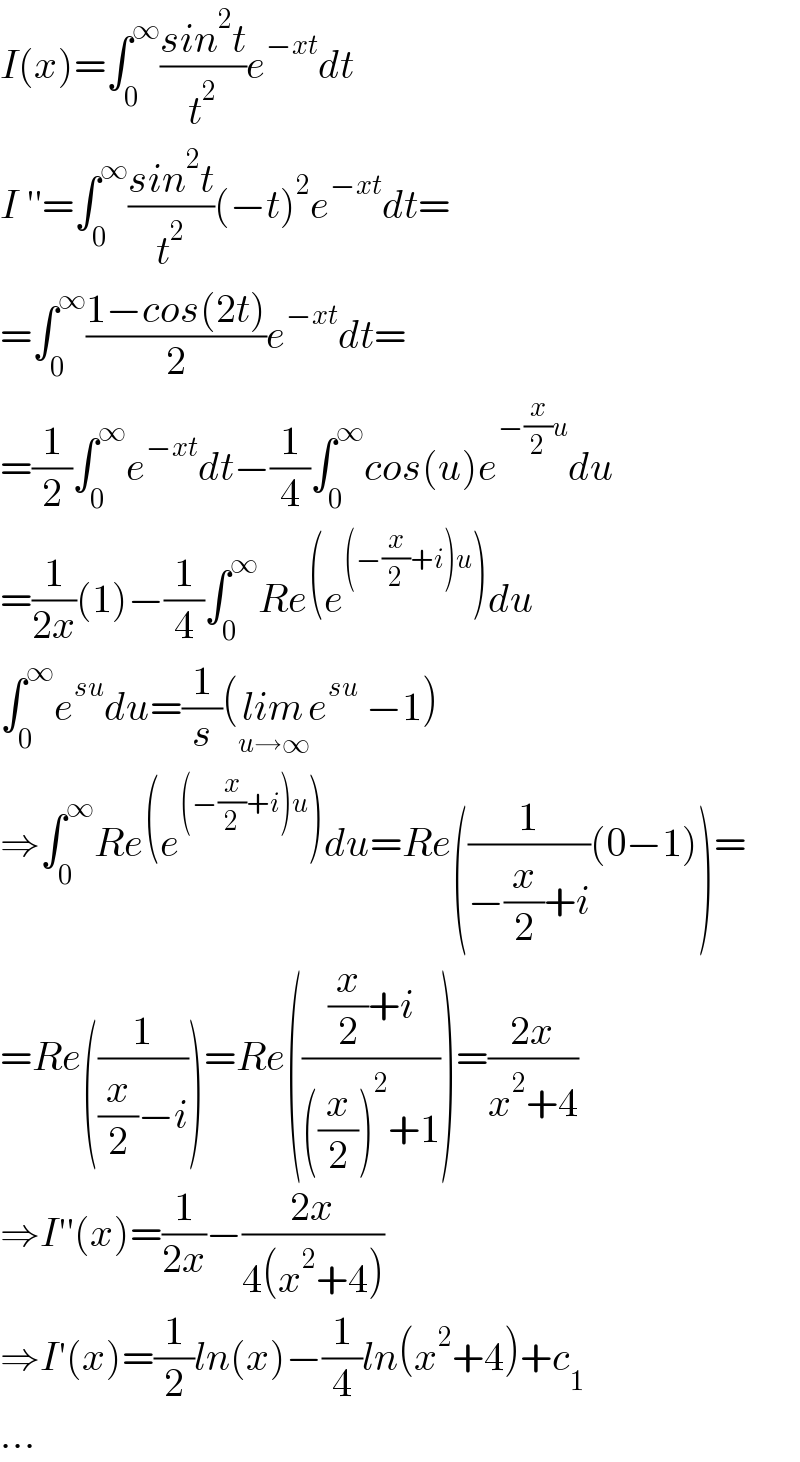
$${I}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} }{e}^{−{xt}} {dt} \\ $$$${I}\:''=\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} }\left(−{t}\right)^{\mathrm{2}} {e}^{−{xt}} {dt}= \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}{e}^{−{xt}} {dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−{xt}} {dt}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {cos}\left({u}\right){e}^{−\frac{{x}}{\mathrm{2}}{u}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{x}}\left(\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {Re}\left({e}^{\left(−\frac{{x}}{\mathrm{2}}+{i}\right){u}} \right){du} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{{su}} {du}=\frac{\mathrm{1}}{{s}}\left(\underset{{u}\rightarrow\infty} {{lim}e}^{{su}} \:−\mathrm{1}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} {Re}\left({e}^{\left(−\frac{{x}}{\mathrm{2}}+{i}\right){u}} \right){du}={Re}\left(\frac{\mathrm{1}}{−\frac{{x}}{\mathrm{2}}+{i}}\left(\mathrm{0}−\mathrm{1}\right)\right)= \\ $$$$={Re}\left(\frac{\mathrm{1}}{\frac{{x}}{\mathrm{2}}−{i}}\right)={Re}\left(\frac{\frac{{x}}{\mathrm{2}}+{i}}{\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}}\right)=\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\Rightarrow{I}''\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{x}}−\frac{\mathrm{2}{x}}{\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$$$\Rightarrow{I}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({x}^{\mathrm{2}} +\mathrm{4}\right)+{c}_{\mathrm{1}} \\ $$$$… \\ $$
