Question Number 13034 by FilupS last updated on 12/May/17

$$\mathrm{MrW1} \\ $$$$\: \\ $$$$\mathrm{Before}\:\mathrm{we}\:\mathrm{concluded}\:\mathrm{that}: \\ $$$$\Phi=\underset{{x}=\mathrm{0}} {\overset{{m}} {\sum}}\underset{{y}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{1}−\mathrm{sgn}\left({x}−{x}'\right)\right) \\ $$$$\: \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{do}: \\ $$$$\underset{{x}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\underset{{y}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\left(\mathrm{1}−\mathrm{sgn}\left({x}−{x}'\right)\right) \\ $$$$=\underset{{x}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\underset{{y}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\left(\mathrm{1}−\mathrm{sgn}\left({x}−\frac{\mathrm{LCM}\left({x},{y}\right)}{{y}}\right)\right) \\ $$$$=\left(\mathrm{1}−\mathrm{sgn}\left(\mathrm{0}−\frac{\mathrm{LCM}\left(\mathrm{0},\mathrm{0}\right)}{\mathrm{0}}\right)\right)+\left(\mathrm{1}−\mathrm{sgn}\left(\mathrm{1}−\frac{\mathrm{LCM}\left(\mathrm{1},\mathrm{0}\right)}{\mathrm{0}}\right)\right. \\ $$$$+\left(\mathrm{1}−\mathrm{sgn}\left(\mathrm{0}−\frac{\mathrm{LCM}\left(\mathrm{0},\mathrm{1}\right)}{\mathrm{1}}\right)\right)+\left(\mathrm{1}−\mathrm{sgn}\left(\mathrm{1}−\frac{\mathrm{LCM}\left(\mathrm{1},\mathrm{1}\right)}{\mathrm{1}}\right)\right. \\ $$$$\: \\ $$$$=\left(\mathrm{1}−\mathrm{sgn}\left(−\frac{\mathrm{LCM}\left(\mathrm{0},\mathrm{0}\right)}{\mathrm{0}}\right)\right)+\left(\mathrm{1}−\mathrm{sgn}\left(\mathrm{1}−\frac{\mathrm{0}}{\mathrm{0}}\right)\right) \\ $$$$+\left(\mathrm{1}−\mathrm{sgn}\left(−\frac{\mathrm{0}}{\mathrm{1}}\right)\right)+\left(\mathrm{1}−\mathrm{sgn}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}}\right)\right) \\ $$$$\: \\ $$$$=???? \\ $$
Commented by mrW1 last updated on 12/May/17

$${the}\:{points}\:{on}\:{the}\:{coordinate}\:{axes}\:{must} \\ $$$${be}\:{excluded},\:{you}\:{can}\:{not}\:{build}\:{fraction} \\ $$$${with}\:\mathrm{0}\:{as}\:{denominator}. \\ $$
Commented by mrW1 last updated on 12/May/17
![for −u≤x≤m and -v≤y≤n the answer is Φ=4+mn−Σ_(i=1) ^m Σ_(j=1) ^n sign[GCD(i,j)−1] +un−Σ_(i=1) ^u Σ_(j=1) ^n sign[GCD(i,j)−1] +uv−Σ_(i=1) ^u Σ_(j=1) ^v sign[GCD(i,j)−1] +mv−Σ_(i=1) ^m Σ_(j=1) ^v sign[GCD(i,j)−1]](https://www.tinkutara.com/question/Q13036.png)
$${for}\:−{u}\leqslant{x}\leqslant{m}\:{and}\:-{v}\leqslant{y}\leqslant{n} \\ $$$${the}\:{answer}\:{is} \\ $$$$\Phi=\mathrm{4}+{mn}−\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}{sign}\left[{GCD}\left({i},{j}\right)−\mathrm{1}\right] \\ $$$$+{un}−\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}{sign}\left[{GCD}\left({i},{j}\right)−\mathrm{1}\right] \\ $$$$+{uv}−\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}{sign}\left[{GCD}\left({i},{j}\right)−\mathrm{1}\right] \\ $$$$+{mv}−\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}{sign}\left[{GCD}\left({i},{j}\right)−\mathrm{1}\right] \\ $$
Commented by FilupS last updated on 12/May/17
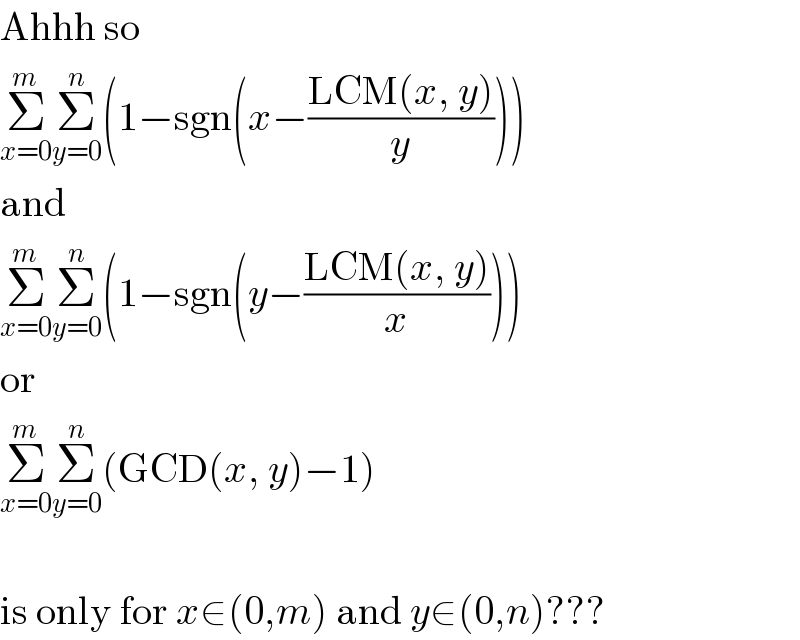
$$\mathrm{Ahhh}\:\mathrm{so} \\ $$$$\underset{{x}=\mathrm{0}} {\overset{{m}} {\sum}}\underset{{y}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{1}−\mathrm{sgn}\left({x}−\frac{\mathrm{LCM}\left({x},\:{y}\right)}{{y}}\right)\right) \\ $$$$\mathrm{and} \\ $$$$\underset{{x}=\mathrm{0}} {\overset{{m}} {\sum}}\underset{{y}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{1}−\mathrm{sgn}\left({y}−\frac{\mathrm{LCM}\left({x},\:{y}\right)}{{x}}\right)\right) \\ $$$$\mathrm{or} \\ $$$$\underset{{x}=\mathrm{0}} {\overset{{m}} {\sum}}\underset{{y}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{GCD}\left({x},\:{y}\right)−\mathrm{1}\right) \\ $$$$\: \\ $$$$\mathrm{is}\:\mathrm{only}\:\mathrm{for}\:{x}\in\left(\mathrm{0},{m}\right)\:\mathrm{and}\:{y}\in\left(\mathrm{0},{n}\right)??? \\ $$
Commented by mrW1 last updated on 12/May/17
![for x∈(0,m] and y∈(0,n] Since on the coordinate axes it happens that tan θ=∞, thus we must exclude them.](https://www.tinkutara.com/question/Q13038.png)
$$\mathrm{for}\:{x}\in\left(\mathrm{0},{m}\right]\:\mathrm{and}\:{y}\in\left(\mathrm{0},{n}\right] \\ $$$${Since}\:{on}\:{the}\:{coordinate}\:{axes}\:{it}\:{happens} \\ $$$${that}\:\mathrm{tan}\:\theta=\infty,\:{thus}\:{we}\:{must}\:{exclude} \\ $$$${them}. \\ $$
