Question Number 121928 by Dwaipayan Shikari last updated on 12/Nov/20

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{12}{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{12}{n}+\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{12}{n}+\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{12}{n}+\mathrm{11}}\right) \\ $$$$ \\ $$$${Problem}\:{source}\::\:{Brilliant}.{Org} \\ $$
Commented by Dwaipayan Shikari last updated on 12/Nov/20
https://brilliant.org/problems/not-quite-a-telescoping-sum-2
https://brilliant.org/problems/integral-out-of-the-box
Commented by Dwaipayan Shikari last updated on 12/Nov/20
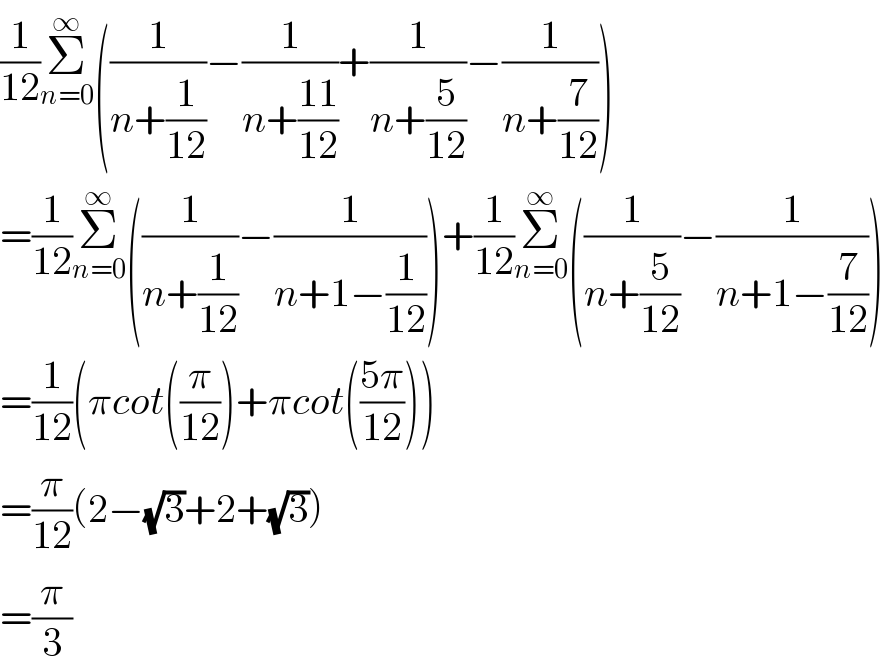
$$\frac{\mathrm{1}}{\mathrm{12}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{12}}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{11}}{\mathrm{12}}}+\frac{\mathrm{1}}{{n}+\frac{\mathrm{5}}{\mathrm{12}}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{7}}{\mathrm{12}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{12}}}−\frac{\mathrm{1}}{{n}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{12}}}\right)+\frac{\mathrm{1}}{\mathrm{12}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\frac{\mathrm{5}}{\mathrm{12}}}−\frac{\mathrm{1}}{{n}+\mathrm{1}−\frac{\mathrm{7}}{\mathrm{12}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left(\pi{cot}\left(\frac{\pi}{\mathrm{12}}\right)+\pi{cot}\left(\frac{\mathrm{5}\pi}{\mathrm{12}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{12}}\left(\mathrm{2}−\sqrt{\mathrm{3}}+\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$=\frac{\pi}{\mathrm{3}} \\ $$
Answered by mnjuly1970 last updated on 12/Nov/20

$${solution}: \\ $$$${S}=\underset{{n}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{12}{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{12}{n}+\mathrm{11}}\right)+\underset{{n}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{12}{n}+\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{12}{n}+\mathrm{7}}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{12}}\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}−\frac{\mathrm{11}}{\mathrm{12}}}−\frac{\mathrm{1}}{{n}−\frac{\mathrm{1}}{\mathrm{12}}}\right)+\frac{\mathrm{1}}{\mathrm{12}}\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}−\frac{\mathrm{7}}{\mathrm{12}}}−\frac{\mathrm{1}}{{n}−\frac{\mathrm{5}}{\mathrm{12}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left(\psi\left(\frac{\mathrm{11}}{\mathrm{12}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{12}}\right)\right)+\frac{\mathrm{1}}{\mathrm{12}}\left(\psi\left(\frac{\mathrm{7}}{\mathrm{12}\:}\right)−\psi\left(\frac{\mathrm{5}}{\mathrm{12}}\right)\right) \\ $$$$\:{we}\:{know}\:{that}: \\ $$$$\:\:\:\psi\left(\mathrm{1}−{s}\right)−\psi\left({s}\right)=\pi{cot}\left(\pi{s}\right) \\ $$$$\therefore\:\:{S}=\frac{\pi}{\mathrm{12}}\left({cot}\left(\frac{\pi}{\mathrm{12}}\right)+{cot}\left(\frac{\mathrm{5}\pi}{\mathrm{12}}\right)\right) \\ $$$$\:\:\:\:\:\:{note}::\:{tan}\left(\mathrm{15}^{°} \right)=\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}{\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}=\frac{\mathrm{12}−\mathrm{6}\sqrt{\mathrm{3}}}{\mathrm{6}}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\:\:{S}=\frac{\pi}{\mathrm{12}}\left(\mathrm{2}+\sqrt{\mathrm{3}}\:+\mathrm{2}−\sqrt{\mathrm{3}}\:\right)=\frac{\pi}{\mathrm{3}} \\ $$$$\:\:\:\:{i}\:{don}'{t}\:{know}\:{finall}\:{answer} \\ $$$$\:\:\:{is}\:{correct}\:\:{or}\:{no}\:\:{please}\:{tell}\:{me}. \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 12/Nov/20
$${Yes}\:{it}\:{is}\:{correct}\:{sir}! \\ $$
Commented by mnjuly1970 last updated on 12/Nov/20
$${thank}\:{you}\:{so}\:{much} \\ $$$${your}\:{questions}\:{is}\:{very}\:{nice}\: \\ $$$${grateful}\:…. \\ $$
