Menu Close

n-0-1-3n-1-3-13-27-3-2-3-81-3-

Tinku Tara 0 Comments
Pin




Question Number 99895 by bachamohamed last updated on 23/Jun/20
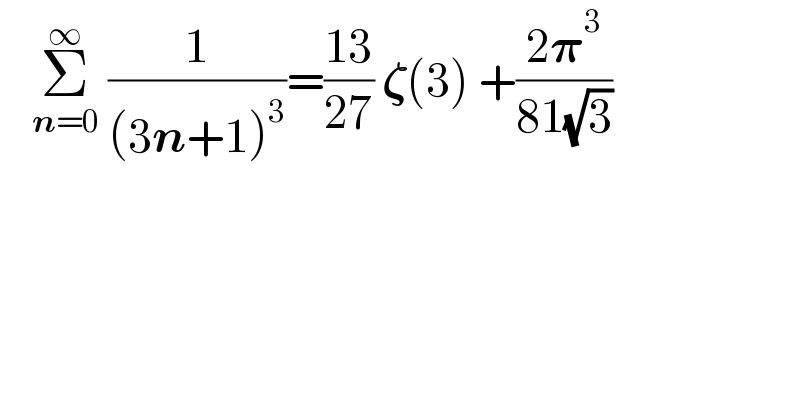
Σ_(n=0) ^∞ (1/((3n+1)^3 ))=((13)/(27)) 𝛇(3) +((2𝛑^3 )/(81(√3)))
$$\:\:\:\:\underset{\boldsymbol{{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{3}\boldsymbol{{n}}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{13}}{\mathrm{27}}\:\boldsymbol{\zeta}\left(\mathrm{3}\right)\:+\frac{\mathrm{2}\boldsymbol{\pi}^{\mathrm{3}} }{\mathrm{81}\sqrt{\mathrm{3}}}\: \\ $$
Answered by maths mind last updated on 24/Jun/20
πcot(πx)=(1/x)+Σ_(n≥1) ((1/(x−n))+(1/(x+n))) ⇒−π^2 (1+cot^2 (πx))=−(1/x^2 )+Σ_(n≥1) (−(1/((x−n)^2 ))−(1/((x+n)^2 ))) ⇒2π^3 (1+cot^2 (πx))cot(πx)=(2/x^3 )+Σ_(n≥1) ((2/((x−n)^3 ))+(2/((x+n)^3 )))...E x=(1/3)⇒ π^3 (4/( (√3)))=54+Σ_(n≥1) (((54)/((1+3n)^3 ))−((54)/((3n−1)^3 )))...E Σ_(n≥1) {(1/((3n−1)^3 ))+(1/((3n)^3 ))+(1/((3n−2)^3 ))}=ζ(3) ⇒Σ_(n≥1) (1/((3n−1)^3 ))+(1/((3n−2)^3 ))=ζ(3)−((ζ(3))/(27))=((26ζ(3))/(27)) ⇒Σ_(n≥0) (1/((3n+2)^3 ))=((26ζ(3))/(27))−Σ_(n≥0) (1/((3n+1)^3 )) Σ_(n≥0) (1/((3n+2)))=Σ_(n≥1) (1/((3n−1)^3 )) ⇒E⇔π^3 (8/(3(√3)))=54+54{Σ_(n≥1) (1/((3n+1)^3 ))−(((26ζ(3))/(27))−Σ_(n≥0) (1/((3n+1)^3 )))} ⇒π^3 (8/(3(√3))) =54+54{Σ_(n≥1) (1/((3n+1)^3 ))−((26ζ(3))/(27))+1+Σ_(n≥1) (1/((3n+1)^3 ))} ⇔108Σ_(n≥1) (1/((3n+1)^3 ))+108=π^3 4(√3)+52ζ(3)...R Σ_(n≥1) (1/((3n+1)^3 ))=^� Σ_(n≥0) (1/((3n+1)^3 ))−1⇒R⇔108Σ_(n≥1) (1/((3n+1)^3 ))=((8π^3 )/(3(√3)))+52ζ(3) Σ(1/((3n+1)^3 ))=((π^3 8)/(108.3(√3)))+((52ζ(3))/(108)) Σ_(m∈N) (1/((3m+1)^3 ))=((13)/(27))ζ(3)+((2π^3 )/(81(√3)))
$$\pi{cot}\left(\pi{x}\right)=\frac{\mathrm{1}}{{x}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{x}−{n}}+\frac{\mathrm{1}}{{x}+{n}}\right) \\ $$$$\Rightarrow−\pi^{\mathrm{2}} \left(\mathrm{1}+{cot}^{\mathrm{2}} \left(\pi{x}\right)\right)=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\frac{\mathrm{1}}{\left({x}−{n}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({x}+{n}\right)^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\mathrm{2}\pi^{\mathrm{3}} \left(\mathrm{1}+{cot}^{\mathrm{2}} \left(\pi{x}\right)\right){cot}\left(\pi{x}\right)=\frac{\mathrm{2}}{{x}^{\mathrm{3}} }+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{2}}{\left({x}−{n}\right)^{\mathrm{3}} }+\frac{\mathrm{2}}{\left({x}+{n}\right)^{\mathrm{3}} }\right)…{E} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow \\ $$$$\pi^{\mathrm{3}} \frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}=\mathrm{54}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{54}}{\left(\mathrm{1}+\mathrm{3}{n}\right)^{\mathrm{3}} }−\frac{\mathrm{54}}{\left(\mathrm{3}{n}−\mathrm{1}\right)^{\mathrm{3}} }\right)…{E} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\left\{\frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{2}\right)^{\mathrm{3}} }\right\}=\zeta\left(\mathrm{3}\right) \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{2}\right)^{\mathrm{3}} }=\zeta\left(\mathrm{3}\right)−\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{27}}=\frac{\mathrm{26}\zeta\left(\mathrm{3}\right)}{\mathrm{27}} \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{2}\right)^{\mathrm{3}} }=\frac{\mathrm{26}\zeta\left(\mathrm{3}\right)}{\mathrm{27}}−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{2}\right)}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\Rightarrow{E}\Leftrightarrow\pi^{\mathrm{3}} \frac{\mathrm{8}}{\mathrm{3}\sqrt{\mathrm{3}}}=\mathrm{54}+\mathrm{54}\left\{\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }−\left(\frac{\mathrm{26}\zeta\left(\mathrm{3}\right)}{\mathrm{27}}−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }\right)\right\} \\ $$$$\Rightarrow\pi^{\mathrm{3}} \frac{\mathrm{8}}{\mathrm{3}\sqrt{\mathrm{3}}}\:=\mathrm{54}+\mathrm{54}\left\{\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{26}\zeta\left(\mathrm{3}\right)}{\mathrm{27}}+\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }\right\} \\ $$$$\Leftrightarrow\mathrm{108}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }+\mathrm{108}=\pi^{\mathrm{3}} \mathrm{4}\sqrt{\mathrm{3}}+\mathrm{52}\zeta\left(\mathrm{3}\right)…{R} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }\hat {=}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }−\mathrm{1}\Rightarrow{R}\Leftrightarrow\mathrm{108}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{8}\pi^{\mathrm{3}} }{\mathrm{3}\sqrt{\mathrm{3}}}+\mathrm{52}\zeta\left(\mathrm{3}\right) \\ $$$$\Sigma\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\pi^{\mathrm{3}} \mathrm{8}}{\mathrm{108}.\mathrm{3}\sqrt{\mathrm{3}}}+\frac{\mathrm{52}\zeta\left(\mathrm{3}\right)}{\mathrm{108}} \\ $$$$\underset{{m}\in\mathbb{N}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{m}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{13}}{\mathrm{27}}\zeta\left(\mathrm{3}\right)+\frac{\mathrm{2}\pi^{\mathrm{3}} }{\mathrm{81}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by bachamohamed last updated on 24/Jun/20
thank′s sir
$$\boldsymbol{{thank}}'\mathrm{s}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *