n-0-1-3n-1-3n-2-

Question Number 157120 by cortano last updated on 20/Oct/21

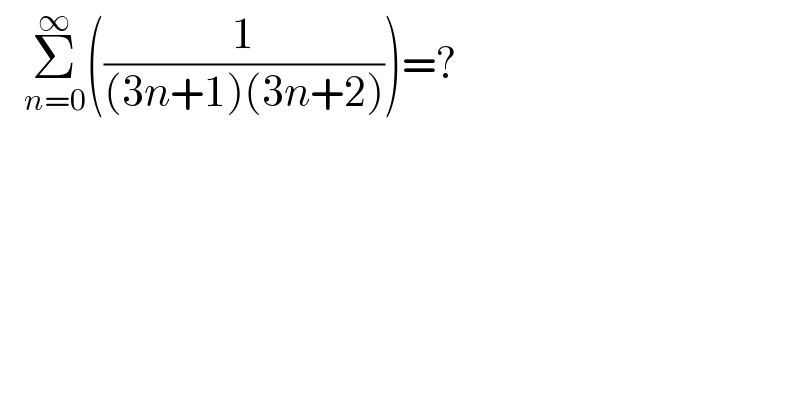
$$\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}\right)=? \\ $$

Answered by puissant last updated on 20/Oct/21

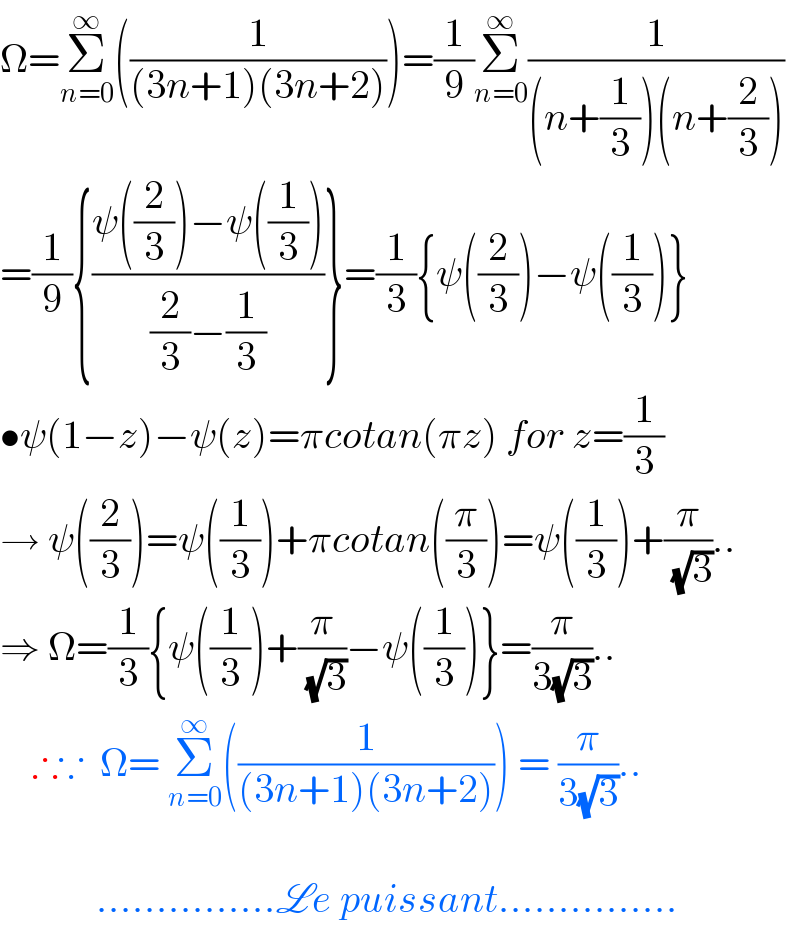
Ω=Σ_(n=0) ^∞ ((1/((3n+1)(3n+2))))=(1/9)Σ_(n=0) ^∞ (1/((n+(1/3))(n+(2/3)))) =(1/9){((ψ((2/3))−ψ((1/3)))/((2/3)−(1/3)))}=(1/3){ψ((2/3))−ψ((1/3))} •ψ(1−z)−ψ(z)=πcotan(πz) for z=(1/3) → ψ((2/3))=ψ((1/3))+πcotan((π/3))=ψ((1/3))+(π/( (√3))).. ⇒ Ω=(1/3){ψ((1/3))+(π/( (√3)))−ψ((1/3))}=(π/(3(√3))).. ∴∵ Ω= Σ_(n=0) ^∞ ((1/((3n+1)(3n+2)))) = (π/(3(√3))).. ...............Le puissant...............

$$\Omega=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}\right)=\frac{\mathrm{1}}{\mathrm{9}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left\{\frac{\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}}\right\}=\frac{\mathrm{1}}{\mathrm{3}}\left\{\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right\} \\ $$$$\bullet\psi\left(\mathrm{1}−{z}\right)−\psi\left({z}\right)=\pi{cotan}\left(\pi{z}\right)\:{for}\:{z}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\rightarrow\:\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\pi{cotan}\left(\frac{\pi}{\mathrm{3}}\right)=\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\pi}{\:\sqrt{\mathrm{3}}}.. \\ $$$$\Rightarrow\:\Omega=\frac{\mathrm{1}}{\mathrm{3}}\left\{\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\pi}{\:\sqrt{\mathrm{3}}}−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right\}=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}.. \\ $$$$\:\:\:\:\therefore\because\:\:\Omega=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}\right)\:=\:\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:……………\mathscr{L}{e}\:{puissant}…………… \\ $$

Commented by Tawa11 last updated on 20/Oct/21

$$\mathrm{great}\:\mathrm{sir} \\ $$

Answered by cortano last updated on 20/Oct/21

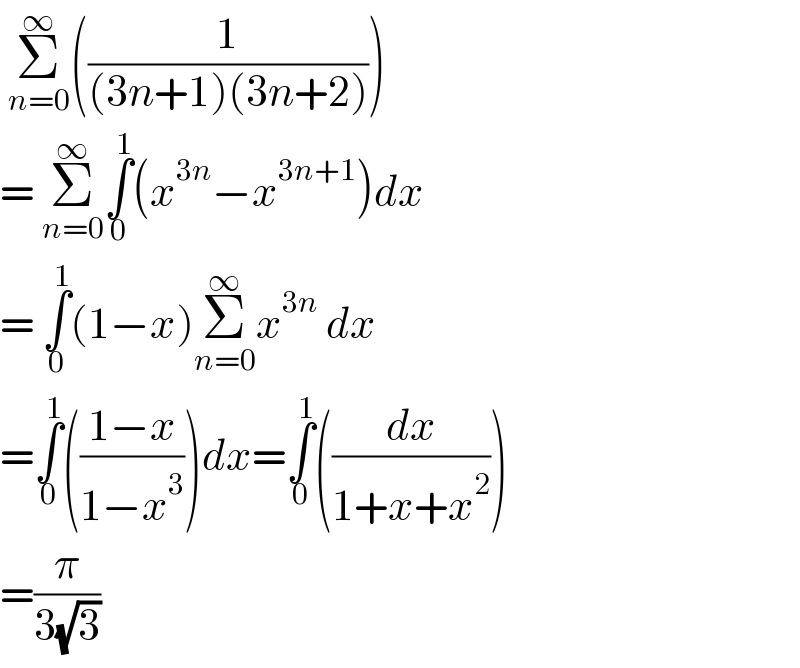
Σ_(n=0) ^∞ ((1/((3n+1)(3n+2)))) = Σ_(n=0) ^∞ ∫_0 ^1 (x^(3n) −x^(3n+1) )dx = ∫_0 ^1 (1−x)Σ_(n=0) ^∞ x^(3n) dx =∫_0 ^1 (((1−x)/(1−x^3 )))dx=∫_0 ^1 ((dx/(1+x+x^2 ))) =(π/(3(√3)))

$$\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}\right) \\ $$$$=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{3}{n}} −{x}^{\mathrm{3}{n}+\mathrm{1}} \right){dx} \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{1}−{x}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{\mathrm{3}{n}} \:{dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}−{x}^{\mathrm{3}} }\right){dx}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\frac{{dx}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\right) \\ $$$$=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply