Question Number 128048 by bramlexs22 last updated on 04/Jan/21

$$\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{8n}+\mathrm{3}}\:=? \\ $$
Answered by Olaf last updated on 04/Jan/21

$$\mathrm{L}\left(\lambda,\alpha,{s}\right)\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{e}^{\mathrm{2}{i}\pi\lambda{n}} }{\left({n}+\alpha\right)^{{s}} }\:\mathrm{or}\:\mathrm{Lerch}\left(\lambda,\alpha,{s}\right) \\ $$$$\left(\mathrm{zeta}\:\mathrm{Lerch}\:\mathrm{function}\right) \\ $$$$\mathrm{Let}\:\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{8}{n}+\mathrm{3}} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{e}^{{i}\pi{n}} }{\left({n}+\frac{\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{1}} }\:=\:\frac{\mathrm{1}}{\mathrm{8}}\mathrm{L}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{8}},\mathrm{1}\right) \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{too}\:: \\ $$$$\Phi\left({z},{s},\alpha\right)\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{z}^{{n}} }{\left({n}+\alpha\right)^{{s}} }\:\mathrm{or}\:\mathrm{LerchPhi}\left({z},{s},\alpha\right) \\ $$$$\left(\mathrm{transcendent}\:\mathrm{Lerch}\:\mathrm{function}\right) \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\frac{\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{1}} }\:=\:\frac{\mathrm{1}}{\mathrm{8}}\Phi\left(−\mathrm{1},\mathrm{1},\frac{\mathrm{3}}{\mathrm{8}}\right) \\ $$$$\mathrm{S}\:\approx\:\mathrm{0},\mathrm{2738982192} \\ $$
Commented by bramlexs22 last updated on 04/Jan/21
I just found out about the lerch zeta function
Commented by bramlexs22 last updated on 04/Jan/21

$$\mathrm{how}\:\mathrm{about}\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{8n}+\mathrm{5}}\:\mathrm{sir}\:? \\ $$
Commented by Olaf last updated on 04/Jan/21

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{8}{n}+\mathrm{5}}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\mathrm{LerchPhi}\left(−\mathrm{1},\mathrm{1},\frac{\mathrm{5}}{\mathrm{8}}\right) \\ $$$$\approx\:\mathrm{0},\mathrm{1511562039} \\ $$
Commented by bramlexs22 last updated on 04/Jan/21
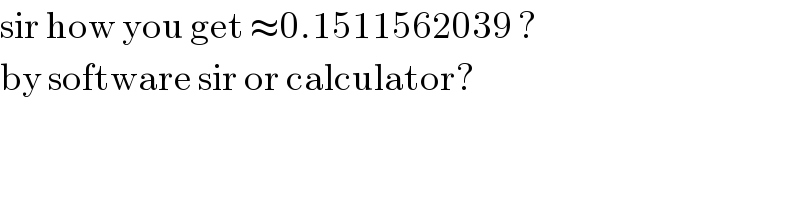
$$\mathrm{sir}\:\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\approx\mathrm{0}.\mathrm{1511562039}\:? \\ $$$$\mathrm{by}\:\mathrm{software}\:\mathrm{sir}\:\mathrm{or}\:\mathrm{calculator}? \\ $$
Answered by mindispower last updated on 04/Jan/21
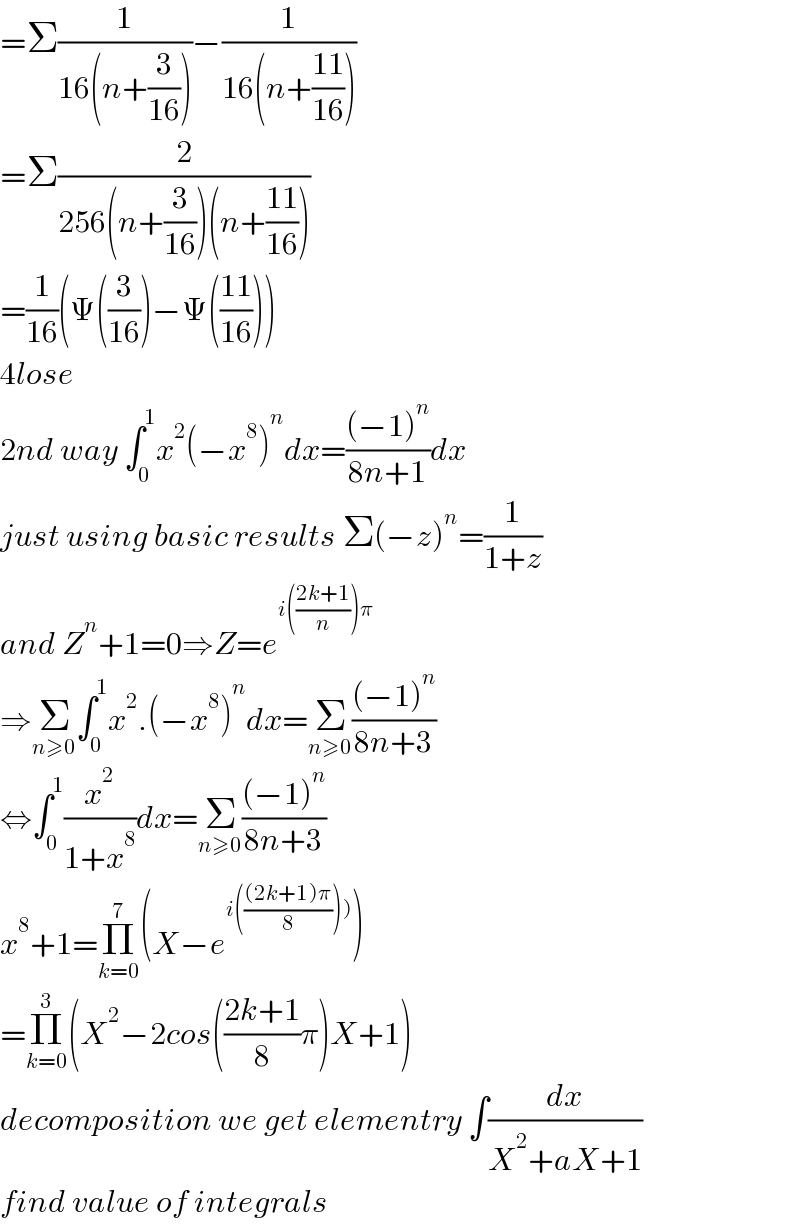
$$=\Sigma\frac{\mathrm{1}}{\mathrm{16}\left({n}+\frac{\mathrm{3}}{\mathrm{16}}\right)}−\frac{\mathrm{1}}{\mathrm{16}\left({n}+\frac{\mathrm{11}}{\mathrm{16}}\right)} \\ $$$$=\Sigma\frac{\mathrm{2}}{\mathrm{256}\left({n}+\frac{\mathrm{3}}{\mathrm{16}}\right)\left({n}+\frac{\mathrm{11}}{\mathrm{16}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\Psi\left(\frac{\mathrm{3}}{\mathrm{16}}\right)−\Psi\left(\frac{\mathrm{11}}{\mathrm{16}}\right)\right) \\ $$$$\mathrm{4}{lose} \\ $$$$\mathrm{2}{nd}\:{way}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \left(−{x}^{\mathrm{8}} \right)^{{n}} {dx}=\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{8}{n}+\mathrm{1}}{dx} \\ $$$${just}\:{using}\:{basic}\:{results}\:\Sigma\left(−{z}\right)^{{n}} =\frac{\mathrm{1}}{\mathrm{1}+{z}} \\ $$$${and}\:{Z}^{{n}} +\mathrm{1}=\mathrm{0}\Rightarrow{Z}={e}^{{i}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\right)\pi} \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} .\left(−{x}^{\mathrm{8}} \right)^{{n}} {dx}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{8}{n}+\mathrm{3}} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{8}} }{dx}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{8}{n}+\mathrm{3}} \\ $$$${x}^{\mathrm{8}} +\mathrm{1}=\underset{{k}=\mathrm{0}} {\overset{\mathrm{7}} {\prod}}\left({X}−{e}^{\left.{i}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{8}}\right)\right)} \right) \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\prod}}\left({X}^{\mathrm{2}} −\mathrm{2}{cos}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{8}}\pi\right){X}+\mathrm{1}\right) \\ $$$${decomposition}\:{we}\:{get}\:{elementry}\:\int\frac{{dx}}{{X}^{\mathrm{2}} +{aX}+\mathrm{1}} \\ $$$${find}\:{value}\:{of}\:{integrals} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Jan/21

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{8}{n}+\mathrm{3}}=\int_{\mathrm{0}} ^{\mathrm{1}} \overset{\infty} {\sum}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{8}{n}+\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{8}} }{dx}\:\:\:{we}\:{can}\:{solve}\:{this}\:{After}\:{decomposing} \\ $$$$ \\ $$
