Menu Close

n-0-1-n-n-1-1-1-3-1-2n-1-

Tinku Tara 0 Comments
Pin




Question Number 146767 by qaz last updated on 15/Jul/21
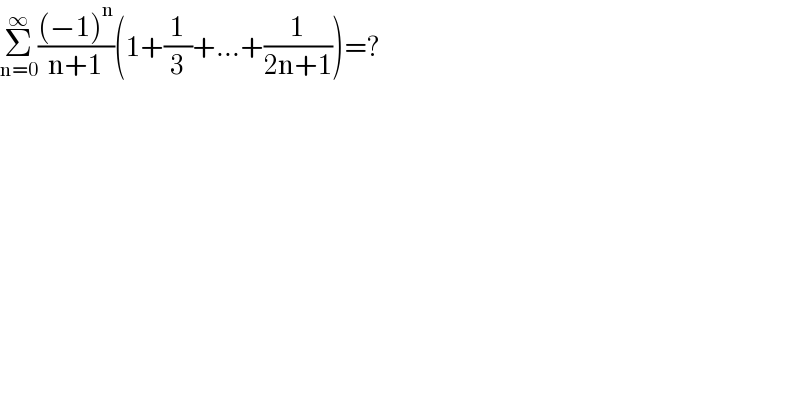
Σ_(n=0) ^∞ (((−1)^n )/(n+1))(1+(1/3)+...+(1/(2n+1)))=?
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\right)=? \\ $$
Answered by mnjuly1970 last updated on 16/Jul/21
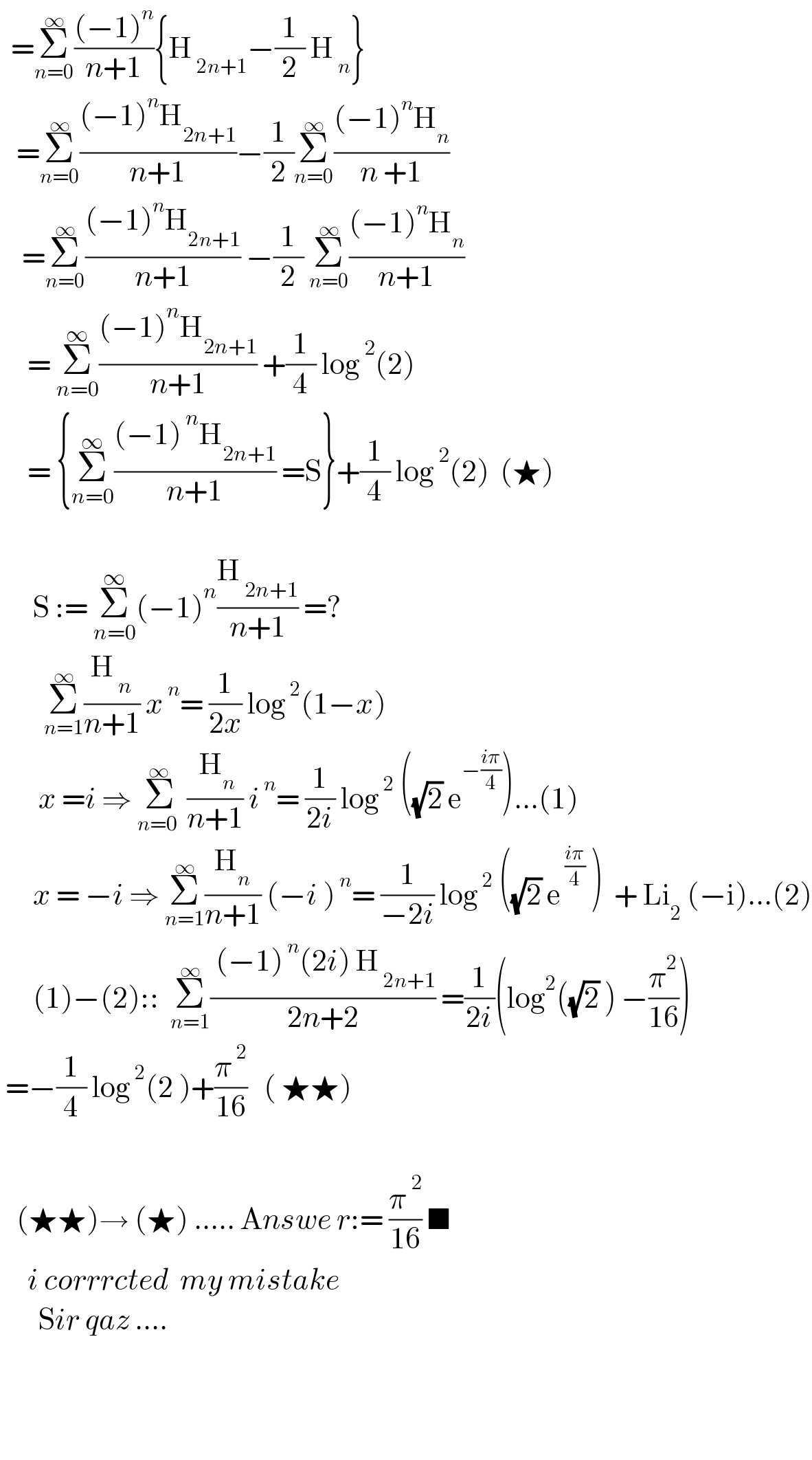
=Σ_(n=0) ^∞ (((−1)^n )/(n+1)){H_( 2n+1) −(1/2) H_( n) } =Σ_(n=0) ^∞ (((−1)^n H_(2n+1) )/(n+1))−(1/2)Σ_(n=0) ^∞ (((−1)^n H_n )/(n +1)) =Σ_(n=0) ^∞ (((−1)^n H_(2n+1) )/(n+1)) −(1/2) Σ_(n=0) ^∞ (((−1)^n H_n )/(n+1)) = Σ_(n=0) ^∞ (((−1)^n H_(2n+1) )/(n+1)) +(1/4) log^( 2) (2) = {Σ_(n=0) ^∞ (((−1)^( n) H_(2n+1) )/(n+1)) =S}+(1/4) log^( 2) (2) (★) S := Σ_(n=0) ^∞ (−1)^n (H_( 2n+1) /(n+1)) =? Σ_(n=1) ^∞ (H_( n) /(n+1)) x^( n) = (1/(2x)) log^( 2) (1−x) x =i ⇒ Σ_(n=0 ) ^∞ (( H_n )/(n+1)) i^( n) = (1/(2i)) log^( 2) ((√2) e^(−((iπ)/4)) )...(1) x = −i ⇒ Σ_(n=1) ^∞ (H_n /(n+1)) (−i )^( n) = (1/(−2i)) log^( 2) ((√2) e^( ((iπ)/4)) ) + Li_2 (−i)...(2) (1)−(2):: Σ_(n=1) ^∞ (( (−1)^( n) (2i) H_( 2n+1) )/(2n+2)) =(1/(2i))(log^2 ((√2) )^ −(π^2 /(16))) =−(1/4) log^( 2) (2 )+(π^( 2) /(16)) ( ★★) (★★)→ (★) ..... Answe r:= (π^( 2) /(16)) ■ i corrrcted my mistake Sir qaz ....
$$\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\left\{\mathrm{H}_{\:\mathrm{2}{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{H}_{\:{n}} \right\}\: \\ $$$$\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{H}_{\mathrm{2}{n}+\mathrm{1}} }{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{H}_{{n}} }{{n}\:+\mathrm{1}} \\ $$$$\:\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{H}_{\mathrm{2}{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{H}_{{n}} }{{n}+\mathrm{1}}\:\: \\ $$$$\:\:\:\:\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{H}_{\mathrm{2}{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{log}^{\:\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:=\:\left\{\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\:{n}} \mathrm{H}_{\mathrm{2}{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=\mathrm{S}\right\}+\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{log}^{\:\mathrm{2}} \left(\mathrm{2}\right)\:\:\left(\bigstar\right) \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\mathrm{S}\::=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{H}_{\:\mathrm{2}{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=? \\ $$$$\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{H}_{\:{n}} }{{n}+\mathrm{1}}\:{x}^{\:{n}} =\:\frac{\mathrm{1}}{\mathrm{2}{x}}\:\mathrm{log}^{\:\mathrm{2}} \left(\mathrm{1}−{x}\right)\: \\ $$$$\:\:\:\:\:\:\:{x}\:={i}\:\Rightarrow\:\underset{{n}=\mathrm{0}\:} {\overset{\infty} {\sum}}\:\frac{\:\mathrm{H}_{{n}} }{{n}+\mathrm{1}}\:{i}^{\:{n}} =\:\frac{\mathrm{1}}{\mathrm{2}{i}}\:\mathrm{log}^{\:\mathrm{2}} \:\left(\sqrt{\mathrm{2}}\:\mathrm{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)…\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:{x}\:=\:−{i}\:\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{H}_{{n}} }{{n}+\mathrm{1}}\:\left(−{i}\:\right)^{\:{n}} =\:\frac{\mathrm{1}}{−\mathrm{2}{i}}\:\mathrm{log}^{\:\mathrm{2}} \:\left(\sqrt{\mathrm{2}}\:\mathrm{e}^{\:\frac{{i}\pi}{\mathrm{4}}} \:\right)\:\:+\:\mathrm{Li}_{\mathrm{2}} \:\left(−\mathrm{i}\right)…\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\left(\mathrm{1}\right)−\left(\mathrm{2}\right)::\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\left(−\mathrm{1}\right)^{\:{n}} \left(\mathrm{2}{i}\right)\:\mathrm{H}_{\:\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\mathrm{log}^{\mathrm{2}} \left(\sqrt{\mathrm{2}}\:\right)^{\:} −\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\right) \\ $$$$\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{log}^{\:\mathrm{2}} \left(\mathrm{2}\:\right)+\frac{\pi^{\:\mathrm{2}} }{\mathrm{16}}\:\:\:\left(\:\bigstar\bigstar\right) \\ $$$$ \\ $$$$\:\:\:\left(\bigstar\bigstar\right)\rightarrow\:\left(\bigstar\right)\:…..\:\mathrm{A}{nswe}\:{r}:=\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{16}}\:\blacksquare \\ $$$$\:\:\:\:\:{i}\:{corrrcted}\:\:{my}\:{mistake} \\ $$$$\:\:\:\:\:\:\:\mathrm{S}{ir}\:{qaz}\:…. \\ $$$$ \\ $$$$\:\:\:\: \\ $$$$\:\:\:\: \\ $$
Commented by qaz last updated on 16/Jul/21
Answer is (π^2 /(16)).Sir
$$\mathrm{Answer}\:\mathrm{is}\:\frac{\pi^{\mathrm{2}} }{\mathrm{16}}.\mathrm{Sir} \\ $$
Commented by qaz last updated on 16/Jul/21
The other′s sol.... Σ_(n=0) ^∞ (((−1)^n )/(n+1))(1+(1/3)+...+(1/(2n+1))) =Σ_(n=0) ^∞ ∫_0 ^1 (((−1)^n (1−x^(2n+2) ))/((n+1)(1−x^2 )))dx =∫_0 ^1 ((ln2−ln(1+x^2 ))/(1−x^2 ))dx =∫_0 ^1 ∫_0 ^1 (1/(2−(1−x^2 )y))dydx =∫_0 ^1 ((tan^(−1) ((√(y/(2−y)))))/( (√(2y−y^2 ))))dy =(tan^(−1) ((√(y/(2−y)))))^2 ∣_0 ^1 =(π^2 /(16)) −−−−−−−−−−−−−−−−−−−−− My sol... Σ_(n=0) ^∞ (((−1)^n )/(n+1))(1+(1/3)+...+(1/(2n+1))) =∫_0 ^1 Σ_(n=0) ^∞ Σ_(k=0) ^n (((−x)^n )/(2k+1))dx =∫_0 ^1 Σ_(k=0) ^∞ Σ_(n=k) ^∞ (((−x)^n )/(2k+1))dx =∫_0 ^1 Σ_(k=0) ^∞ Σ_(n=0) ^∞ (((−x)^(n+k) )/(2k+1))dx =∫_0 ^1 (Σ_(k=0) ^∞ (((−x)^k )/(2k+1)))(Σ_(n=0) ^∞ (−x)^n )dx =∫_0 ^1 (1/(1+x))(Σ_(k=0) ^∞ (−x)^k ∫_0 ^1 y^(2k) dy)dx =∫_0 ^1 (1/(1+x))∫_0 ^1 (1/(1+xy^2 ))dydx =∫_0 ^1 ((tan^(−1) (√x))/((1+x)(√x)))dx =(π^2 /(16))
$$\mathrm{The}\:\mathrm{other}'\mathrm{s}\:\mathrm{sol}…. \\ $$$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\right) \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2n}+\mathrm{2}} \right)}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln2}−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}−\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{y}}\mathrm{dydx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{y}}{\mathrm{2}−\mathrm{y}}}\right)}{\:\sqrt{\mathrm{2y}−\mathrm{y}^{\mathrm{2}} }}\mathrm{dy} \\ $$$$=\left(\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{y}}{\mathrm{2}−\mathrm{y}}}\right)\right)^{\mathrm{2}} \mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$$$−−−−−−−−−−−−−−−−−−−−− \\ $$$$\mathrm{My}\:\mathrm{sol}… \\ $$$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\left(−\mathrm{x}\right)^{\mathrm{n}} }{\mathrm{2k}+\mathrm{1}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{k}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{x}\right)^{\mathrm{n}} }{\mathrm{2k}+\mathrm{1}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{x}\right)^{\mathrm{n}+\mathrm{k}} }{\mathrm{2k}+\mathrm{1}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{x}\right)^{\mathrm{k}} }{\mathrm{2k}+\mathrm{1}}\right)\left(\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{x}\right)^{\mathrm{n}} \right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{x}\right)^{\mathrm{k}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{y}^{\mathrm{2k}} \mathrm{dy}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{xy}^{\mathrm{2}} }\mathrm{dydx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{x}}}{\left(\mathrm{1}+\mathrm{x}\right)\sqrt{\mathrm{x}}}\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$
Commented by mnjuly1970 last updated on 16/Jul/21
thank you so much...
$${thank}\:{you}\:{so}\:{much}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *