Menu Close

n-0-1-n-n-4-n-2-1-

Tinku Tara 0 Comments
Pin




Question Number 159080 by qaz last updated on 12/Nov/21
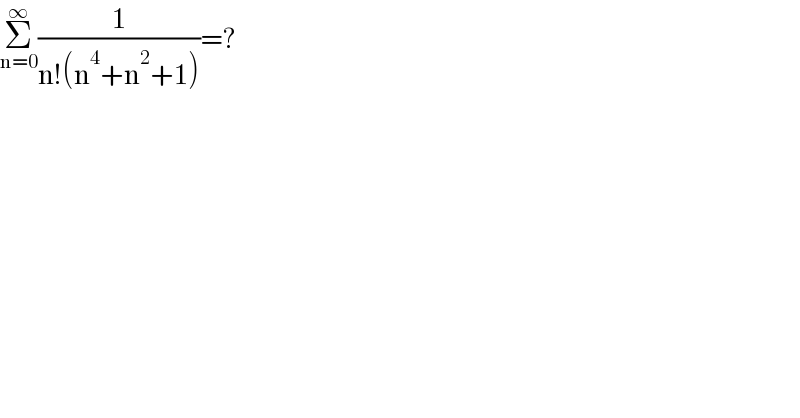
Σ_(n=0) ^∞ (1/(n!(n^4 +n^2 +1)))=?
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}!\left(\mathrm{n}^{\mathrm{4}} +\mathrm{n}^{\mathrm{2}} +\mathrm{1}\right)}=? \\ $$
Answered by mindispower last updated on 13/Nov/21
=Σ_(n≥0) (1/(n!(n^2 +1−n)(n^2 +1+n))) =Σ_(n≥0) (1/(n!))(((an+b)/(n^2 −n+1))+((cn+d)/(n^2 +n+1))) a+c=0,b+d=1,(a+b−c+d)=0,a−c=−1 a=−(1/2),c=(1/2)=b=d =(1/2).Σ_(n≥0) (1/(n!))(.((−n+1)/(n^2 −n+1))+((n+1)/(n^2 +n+1))) =(1/2).Σ_(n≥0) .(1/(n!))(−(n/(n^2 −n+1))+(1/(n^2 +n+1))) =−(1/2)Σ_(n≥1) (1/((n−1)!(n^2 −n+1)_ ))∣_(=U_n ) +(1/2)Σ_(n≥0) (1/(n!(n^2 +n+1))), +(1/2)Σ_(n≥0) (1/(n!))((1/(n^2 −n+1))+(n/(n^2 +n+1))) ={−Σ_(n≥1) (1/2)U_n +Σ_(n≥0) (1/2)U_(n+1) }_(=0) +Σ_(n≥0) (1/(n!(n^2 −n+1)))+(1/2)Σ_(n≥0) (n/(n!(n^2 +n+1))) (n/(n!(n^2 +n+1)))=((n(n+1))/((n+1)!(n^2 +n+1)))=(1/((n+1)!))−(1/((n+1)!(n^2 +n+1))) =(1/2){Σ_(n≥0) (1/(n!(n^2 −n+1)_(.=V_n ) ))+Σ_(n≥0) (1/((n+1)!))−(1/((n+1)!(n^2 +n+1)))} =(1/2)Σ_(n≥0) V_n −Σ_(n≥0) V_(n+1) +(1/2)Σ_(n≥0) (1/((n+1)!))=(V_0 /2)+(1/2)(e−1) V_0 =1 S=(e/2)
$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}!\left({n}^{\mathrm{2}} +\mathrm{1}−{n}\right)\left({n}^{\mathrm{2}} +\mathrm{1}+{n}\right)} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}!}\left(\frac{{an}+{b}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}+\frac{{cn}+{d}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right) \\ $$$${a}+{c}=\mathrm{0},{b}+{d}=\mathrm{1},\left({a}+{b}−{c}+{d}\right)=\mathrm{0},{a}−{c}=−\mathrm{1} \\ $$$${a}=−\frac{\mathrm{1}}{\mathrm{2}},{c}=\frac{\mathrm{1}}{\mathrm{2}}={b}={d} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}!}\left(.\frac{−{n}+\mathrm{1}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}+\frac{{n}+\mathrm{1}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\underset{{n}\geqslant\mathrm{0}} {\sum}.\frac{\mathrm{1}}{{n}!}\left(−\frac{{n}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right)\: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)_{} }\mid_{={U}_{{n}} } +\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}!\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)}, \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}!}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}+\frac{{n}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right) \\ $$$$=\left\{−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{2}}{U}_{{n}} +\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\mathrm{2}}{U}_{{n}+\mathrm{1}} \right\}_{=\mathrm{0}} +\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}!\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{n}}{{n}!\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)} \\ $$$$\frac{{n}}{{n}!\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)}=\frac{{n}\left({n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)!\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}!\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)_{.={V}_{{n}} } }+\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}{V}_{{n}} −\underset{{n}\geqslant\mathrm{0}} {\sum}{V}_{{n}+\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}=\frac{{V}_{\mathrm{0}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\left({e}−\mathrm{1}\right) \\ $$$${V}_{\mathrm{0}} =\mathrm{1} \\ $$$${S}=\frac{{e}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa11 last updated on 13/Nov/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mindispower last updated on 16/Nov/21
thank you sir have nice day
$${thank}\:{you}\:{sir} \\ $$$${have}\:\:{nice}\:{day} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *