Menu Close

n-0-arctan-1-n-2n-1-

Tinku Tara 0 Comments
Pin




Question Number 158822 by qaz last updated on 09/Nov/21
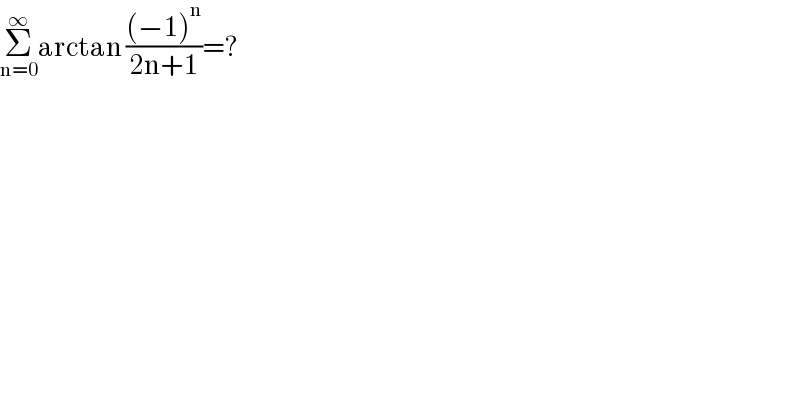
Σ_(n=0) ^∞ arctan (((−1)^n )/(2n+1))=?
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{arctan}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}=? \\ $$
Answered by mindispower last updated on 09/Nov/21
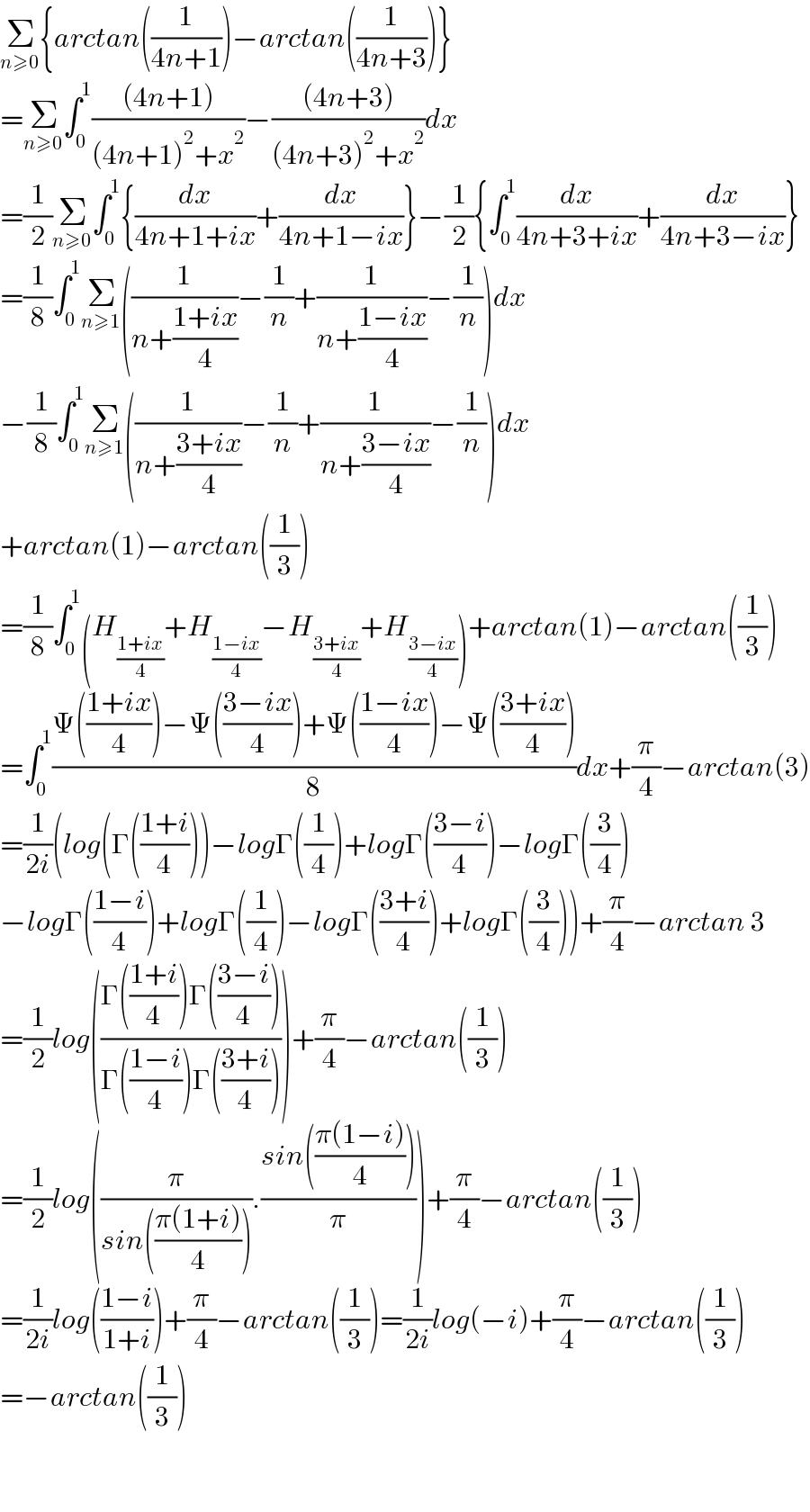
Σ_(n≥0) {arctan((1/(4n+1)))−arctan((1/(4n+3)))} =Σ_(n≥0) ∫_0 ^1 (((4n+1))/((4n+1)^2 +x^2 ))−(((4n+3))/((4n+3)^2 +x^2 ))dx =(1/2)Σ_(n≥0) ∫_0 ^1 {(dx/(4n+1+ix))+(dx/(4n+1−ix))}−(1/2){∫_0 ^1 (dx/(4n+3+ix))+(dx/(4n+3−ix))} =(1/8)∫_0 ^1 Σ_(n≥1) ((1/(n+((1+ix)/4)))−(1/n)+(1/(n+((1−ix)/4)))−(1/n))dx −(1/8)∫_0 ^1 Σ_(n≥1) ((1/(n+((3+ix)/4)))−(1/n)+(1/(n+((3−ix)/4)))−(1/n))dx +arctan(1)−arctan((1/3)) =(1/8)∫_0 ^1 (H_((1+ix)/4) +H_((1−ix)/4) −H_((3+ix)/4) +H_((3−ix)/4) )+arctan(1)−arctan((1/3)) =∫_0 ^1 ((Ψ(((1+ix)/4))−Ψ(((3−ix)/4))+Ψ(((1−ix)/4))−Ψ(((3+ix)/4)))/8)dx+(π/4)−arctan(3) =(1/(2i))(log(Γ(((1+i)/4)))−logΓ((1/4))+logΓ(((3−i)/4))−logΓ((3/4)) −logΓ(((1−i)/4))+logΓ((1/4))−logΓ(((3+i)/4))+logΓ((3/4)))+(π/4)−arctan 3 =(1/2)log(((Γ(((1+i)/4))Γ(((3−i)/4)))/(Γ(((1−i)/4))Γ(((3+i)/4)))))+(π/4)−arctan((1/3)) =(1/2)log((π/(sin(((π(1+i))/4)))).((sin(((π(1−i))/4)))/π))+(π/4)−arctan((1/3)) =(1/(2i))log(((1−i)/(1+i)))+(π/4)−arctan((1/3))=(1/(2i))log(−i)+(π/4)−arctan((1/3)) =−arctan((1/3))
$$\underset{{n}\geqslant\mathrm{0}} {\sum}\left\{{arctan}\left(\frac{\mathrm{1}}{\mathrm{4}{n}+\mathrm{1}}\right)−{arctan}\left(\frac{\mathrm{1}}{\mathrm{4}{n}+\mathrm{3}}\right)\right\} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{4}{n}+\mathrm{1}\right)}{\left(\mathrm{4}{n}+\mathrm{1}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} }−\frac{\left(\mathrm{4}{n}+\mathrm{3}\right)}{\left(\mathrm{4}{n}+\mathrm{3}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{{dx}}{\mathrm{4}{n}+\mathrm{1}+{ix}}+\frac{{dx}}{\mathrm{4}{n}+\mathrm{1}−{ix}}\right\}−\frac{\mathrm{1}}{\mathrm{2}}\left\{\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{4}{n}+\mathrm{3}+{ix}}+\frac{{dx}}{\mathrm{4}{n}+\mathrm{3}−{ix}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}+{ix}}{\mathrm{4}}}−\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}−{ix}}{\mathrm{4}}}−\frac{\mathrm{1}}{{n}}\right){dx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}+\frac{\mathrm{3}+{ix}}{\mathrm{4}}}−\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\frac{\mathrm{3}−{ix}}{\mathrm{4}}}−\frac{\mathrm{1}}{{n}}\right){dx} \\ $$$$+{arctan}\left(\mathrm{1}\right)−{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \left({H}_{\frac{\mathrm{1}+{ix}}{\mathrm{4}}} +{H}_{\frac{\mathrm{1}−{ix}}{\mathrm{4}}} −{H}_{\frac{\mathrm{3}+{ix}}{\mathrm{4}}} +{H}_{\frac{\mathrm{3}−{ix}}{\mathrm{4}}} \right)+{arctan}\left(\mathrm{1}\right)−{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\Psi\left(\frac{\mathrm{1}+{ix}}{\mathrm{4}}\right)−\Psi\left(\frac{\mathrm{3}−{ix}}{\mathrm{4}}\right)+\Psi\left(\frac{\mathrm{1}−{ix}}{\mathrm{4}}\right)−\Psi\left(\frac{\mathrm{3}+{ix}}{\mathrm{4}}\right)}{\mathrm{8}}{dx}+\frac{\pi}{\mathrm{4}}−{arctan}\left(\mathrm{3}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left({log}\left(\Gamma\left(\frac{\mathrm{1}+{i}}{\mathrm{4}}\right)\right)−{log}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)+{log}\Gamma\left(\frac{\mathrm{3}−{i}}{\mathrm{4}}\right)−{log}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right. \\ $$$$\left.−{log}\Gamma\left(\frac{\mathrm{1}−{i}}{\mathrm{4}}\right)+{log}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−{log}\Gamma\left(\frac{\mathrm{3}+{i}}{\mathrm{4}}\right)+{log}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right)+\frac{\pi}{\mathrm{4}}−{arctan}\:\mathrm{3} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\Gamma\left(\frac{\mathrm{1}+{i}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{3}−{i}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{1}−{i}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{3}+{i}}{\mathrm{4}}\right)}\right)+\frac{\pi}{\mathrm{4}}−{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\pi}{{sin}\left(\frac{\pi\left(\mathrm{1}+{i}\right)}{\mathrm{4}}\right)}.\frac{{sin}\left(\frac{\pi\left(\mathrm{1}−{i}\right)}{\mathrm{4}}\right)}{\pi}\right)+\frac{\pi}{\mathrm{4}}−{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left(\frac{\mathrm{1}−{i}}{\mathrm{1}+{i}}\right)+\frac{\pi}{\mathrm{4}}−{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left(−{i}\right)+\frac{\pi}{\mathrm{4}}−{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=−{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mindispower last updated on 10/Nov/21
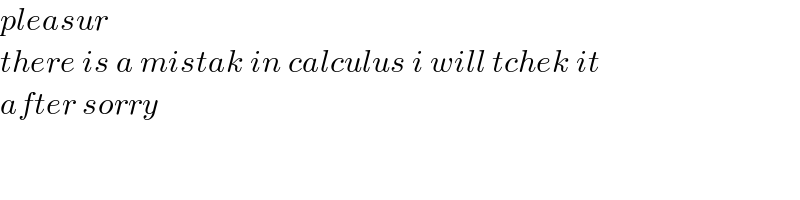
pleasur there is a mistak in calculus i will tchek it after sorry
$${pleasur} \\ $$$${there}\:{is}\:{a}\:{mistak}\:{in}\:{calculus}\:{i}\:{will}\:{tchek}\:{it}\: \\ $$$${after}\:{sorry}\: \\ $$
Commented by qaz last updated on 10/Nov/21
thanks a lot.sir
$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}.\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *