Menu Close

n-0-k-0-n-1-n-pi-e-k-

Tinku Tara 0 Comments
Pin




Question Number 156880 by MathSh last updated on 16/Oct/21
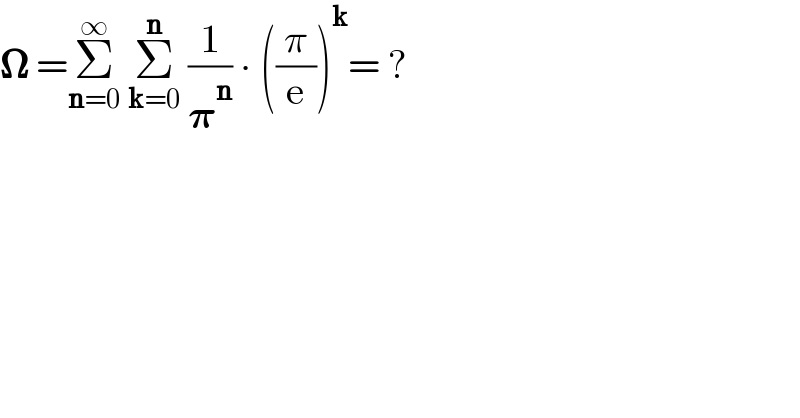
𝛀 =Σ_(n=0) ^∞ Σ_(k=0) ^n (1/𝛑^n ) ∙ ((π/e))^k = ?
$$\boldsymbol{\Omega}\:=\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{0}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\:\frac{\mathrm{1}}{\boldsymbol{\pi}^{\boldsymbol{\mathrm{n}}} }\:\centerdot\:\left(\frac{\pi}{\mathrm{e}}\right)^{\boldsymbol{\mathrm{k}}} =\:? \\ $$
Answered by Mathspace last updated on 16/Oct/21
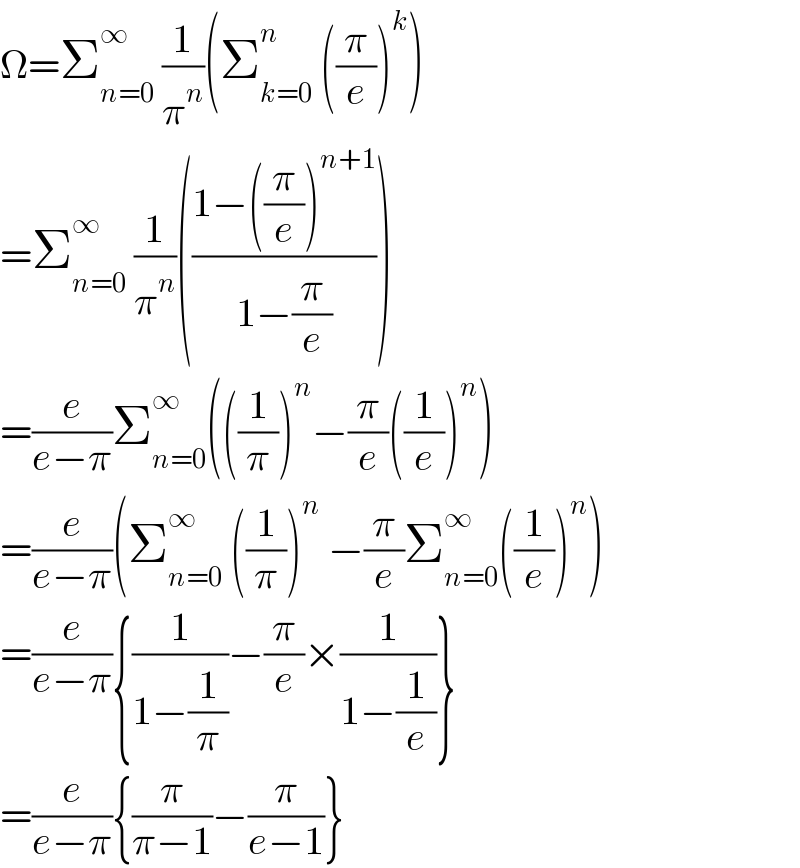
Ω=Σ_(n=0) ^∞ (1/π^n )(Σ_(k=0) ^n ((π/e))^k ) =Σ_(n=0) ^∞ (1/π^n )(((1−((π/e))^(n+1) )/(1−(π/e)))) =(e/(e−π))Σ_(n=0) ^∞ (((1/π))^n −(π/e)((1/e))^n ) =(e/(e−π))(Σ_(n=0) ^∞ ((1/π))^n −(π/e)Σ_(n=0) ^(∞ ) ((1/e))^n ) =(e/(e−π)){(1/(1−(1/π)))−(π/e)×(1/(1−(1/e)))} =(e/(e−π)){(π/(π−1))−(π/(e−1))}
$$\Omega=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\pi^{{n}} }\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(\frac{\pi}{{e}}\right)^{{k}} \right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\pi^{{n}} }\left(\frac{\mathrm{1}−\left(\frac{\pi}{{e}}\right)^{{n}+\mathrm{1}} }{\mathrm{1}−\frac{\pi}{{e}}}\right) \\ $$$$=\frac{{e}}{{e}−\pi}\sum_{{n}=\mathrm{0}} ^{\infty} \left(\left(\frac{\mathrm{1}}{\pi}\right)^{{n}} −\frac{\pi}{{e}}\left(\frac{\mathrm{1}}{{e}}\right)^{{n}} \right) \\ $$$$=\frac{{e}}{{e}−\pi}\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{1}}{\pi}\right)^{{n}} \:−\frac{\pi}{{e}}\sum_{{n}=\mathrm{0}} ^{\infty\:} \left(\frac{\mathrm{1}}{{e}}\right)^{{n}} \right) \\ $$$$=\frac{{e}}{{e}−\pi}\left\{\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\pi}}−\frac{\pi}{{e}}×\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{e}}}\right\} \\ $$$$=\frac{{e}}{{e}−\pi}\left\{\frac{\pi}{\pi−\mathrm{1}}−\frac{\pi}{{e}−\mathrm{1}}\right\} \\ $$
Commented by MathSh last updated on 16/Oct/21
Thank you dear Ser
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Answered by qaz last updated on 16/Oct/21
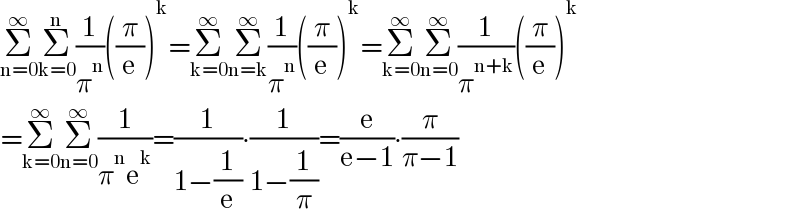
Σ_(n=0) ^∞ Σ_(k=0) ^n (1/π^n )((π/e))^k =Σ_(k=0) ^∞ Σ_(n=k) ^∞ (1/π^n )((π/e))^k =Σ_(k=0) ^∞ Σ_(n=0) ^∞ (1/π^(n+k) )((π/e))^k =Σ_(k=0) ^∞ Σ_(n=0) ^∞ (1/(π^n e^k ))=(1/(1−(1/e)))∙(1/(1−(1/π)))=(e/(e−1))∙(π/(π−1))
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\pi^{\mathrm{n}} }\left(\frac{\pi}{\mathrm{e}}\right)^{\mathrm{k}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{k}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\pi^{\mathrm{n}} }\left(\frac{\pi}{\mathrm{e}}\right)^{\mathrm{k}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\pi^{\mathrm{n}+\mathrm{k}} }\left(\frac{\pi}{\mathrm{e}}\right)^{\mathrm{k}} \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\pi^{\mathrm{n}} \mathrm{e}^{\mathrm{k}} }=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}}\centerdot\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\pi}}=\frac{\mathrm{e}}{\mathrm{e}−\mathrm{1}}\centerdot\frac{\pi}{\pi−\mathrm{1}} \\ $$
Commented by MathSh last updated on 16/Oct/21
Very nice dear Ser thank you
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *