Question Number 61724 by aliesam last updated on 07/Jun/19

$$\underset{{n}\geqslant\mathrm{0}} {\sum}{n}^{\mathrm{2}} {x}^{{n}} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 07/Jun/19
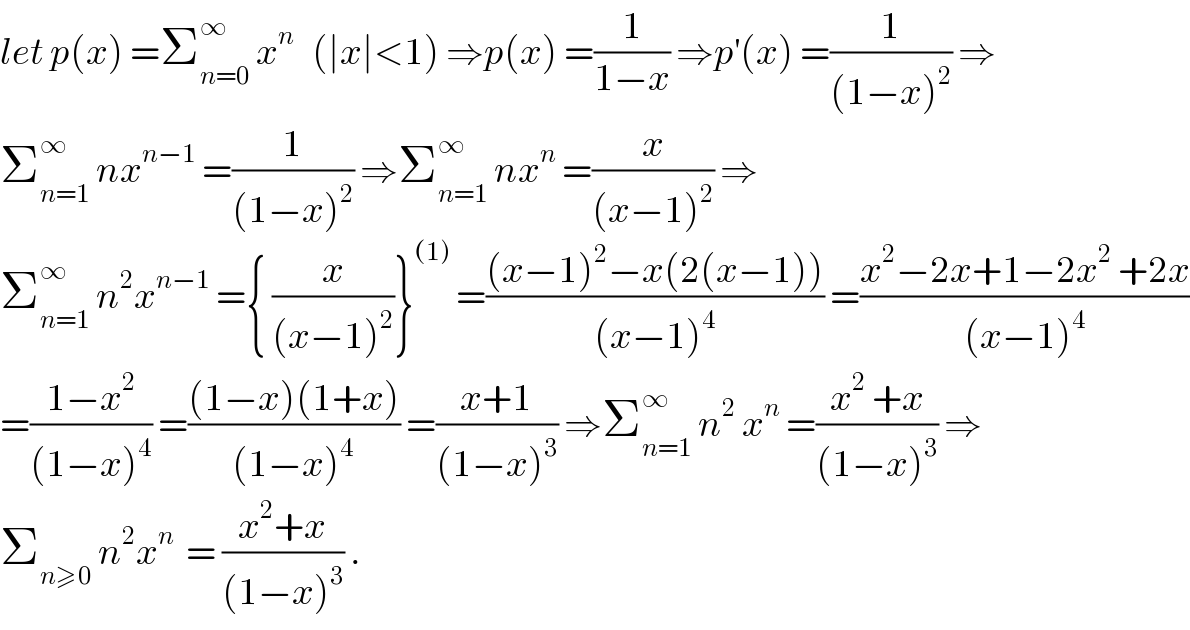
$${let}\:{p}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:\:\:\left(\mid{x}\mid<\mathrm{1}\right)\:\Rightarrow{p}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\Rightarrow{p}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}} \:=\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} \:=\left\{\:\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \:=\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} −{x}\left(\mathrm{2}\left({x}−\mathrm{1}\right)\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{4}} }\:=\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }\:=\frac{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }\:=\frac{{x}+\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} \:{x}^{{n}} \:=\frac{{x}^{\mathrm{2}} \:+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\sum_{{n}\geqslant\mathrm{0}} \:{n}^{\mathrm{2}} {x}^{{n}} \:\:=\:\frac{{x}^{\mathrm{2}} +{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:. \\ $$
Commented by maxmathsup by imad last updated on 07/Jun/19

$${sir}\:\:{aliissam}\:{where}\:{are}\:{you}\:{from}…. \\ $$
Commented by aliesam last updated on 07/Jun/19

$${iraq}\:{sir}\: \\ $$
Commented by aliesam last updated on 07/Jun/19

$${but}\:{why}\: \\ $$
Commented by maxmathsup by imad last updated on 07/Jun/19

$${for}\:{nothing}\:{its}\:{only}\:{a}\:{information}\:{sir}\:…{hou}\:{are}\:{always}\:{welcome}… \\ $$
Commented by aliesam last updated on 07/Jun/19
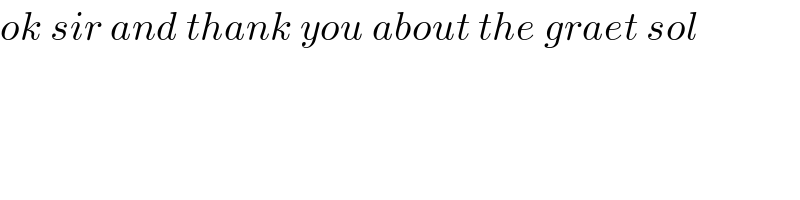
$${ok}\:{sir}\:{and}\:{thank}\:{you}\:{about}\:{the}\:{graet}\:{sol} \\ $$
