Menu Close

n-0-tan-1-n-1-2-tan-1-n-1-2-

Tinku Tara 0 Comments
Pin




Question Number 30929 by rahul 19 last updated on 28/Feb/18
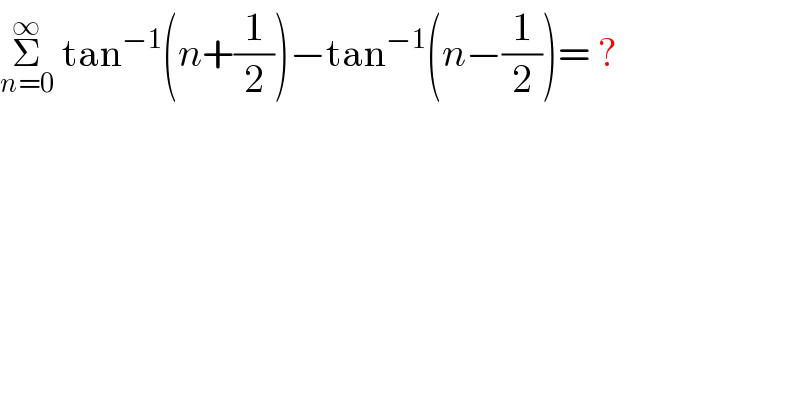
Σ_(n=0) ^∞ tan^(−1) (n+(1/2))−tan^(−1) (n−(1/2))= ?
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\mathrm{tan}^{−\mathrm{1}} \left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{tan}^{−\mathrm{1}} \left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\:? \\ $$
Commented by abdo imad last updated on 01/Mar/18
let put S_n = Σ_(k=0) ^n arctan(k+(1/2))−arctan(k−(1/2)) S_n =Σ_(k=0) ^n arctan(((2k+1)/2))−actan(((2k−1)/2)) =Σ_(k=0) ^n (v_k −v_(k−1) ) with v_k =arctan(((2k+1)/2)) S_n =v_0 −v_(−1) +v_1 −v_o +...+v_n −v_(n−1) =v_n −v_(−1) ⇒ S_n =arctan(((2n+1)/2)) −arctan(−(1/2)) ⇒ lim_(n→∞) S_n = (π/2) +arctan((1/2))=(π/2) +(π/2) −arctan2 =π −arctan2 .
$${let}\:{put}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{arctan}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)−{arctan}\left({k}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} {arctan}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{2}}\right)−{actan}\left(\frac{\mathrm{2}{k}−\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({v}_{{k}} \:−{v}_{{k}−\mathrm{1}} \right)\:{with}\:{v}_{{k}} ={arctan}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$${S}_{{n}} ={v}_{\mathrm{0}} \:−{v}_{−\mathrm{1}} \:+{v}_{\mathrm{1}} \:−{v}_{{o}} \:+…+{v}_{{n}} \:−{v}_{{n}−\mathrm{1}} ={v}_{{n}} \:−{v}_{−\mathrm{1}} \:\Rightarrow \\ $$$${S}_{{n}} ={arctan}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right)\:−{arctan}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow\infty} \:{S}_{{n}} =\:\frac{\pi}{\mathrm{2}}\:+{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{2}}\:−{arctan}\mathrm{2} \\ $$$$=\pi\:−{arctan}\mathrm{2}\:. \\ $$
Answered by sma3l2996 last updated on 28/Feb/18
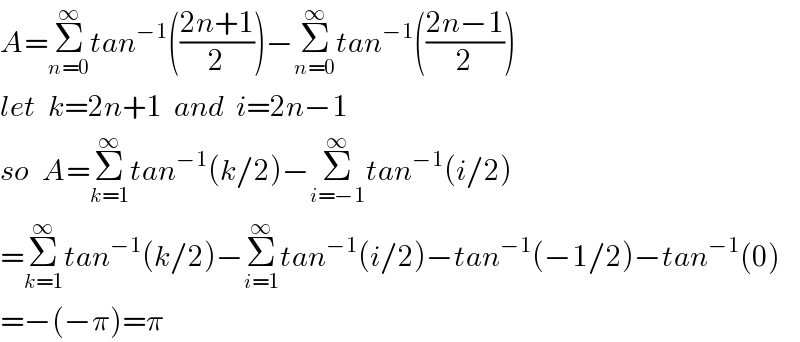
A=Σ_(n=0) ^∞ tan^(−1) (((2n+1)/2))−Σ_(n=0) ^∞ tan^(−1) (((2n−1)/2)) let k=2n+1 and i=2n−1 so A=Σ_(k=1) ^∞ tan^(−1) (k/2)−Σ_(i=−1) ^∞ tan^(−1) (i/2) =Σ_(k=1) ^∞ tan^(−1) (k/2)−Σ_(i=1) ^∞ tan^(−1) (i/2)−tan^(−1) (−1/2)−tan^(−1) (0) =−(−π)=π
$${A}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right)−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\right) \\ $$$${let}\:\:{k}=\mathrm{2}{n}+\mathrm{1}\:\:{and}\:\:{i}=\mathrm{2}{n}−\mathrm{1} \\ $$$${so}\:\:{A}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{tan}^{−\mathrm{1}} \left({k}/\mathrm{2}\right)−\underset{{i}=−\mathrm{1}} {\overset{\infty} {\sum}}{tan}^{−\mathrm{1}} \left({i}/\mathrm{2}\right) \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{tan}^{−\mathrm{1}} \left({k}/\mathrm{2}\right)−\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{tan}^{−\mathrm{1}} \left({i}/\mathrm{2}\right)−{tan}^{−\mathrm{1}} \left(−\mathrm{1}/\mathrm{2}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{0}\right) \\ $$$$=−\left(−\pi\right)=\pi \\ $$
Answered by ajfour last updated on 28/Feb/18
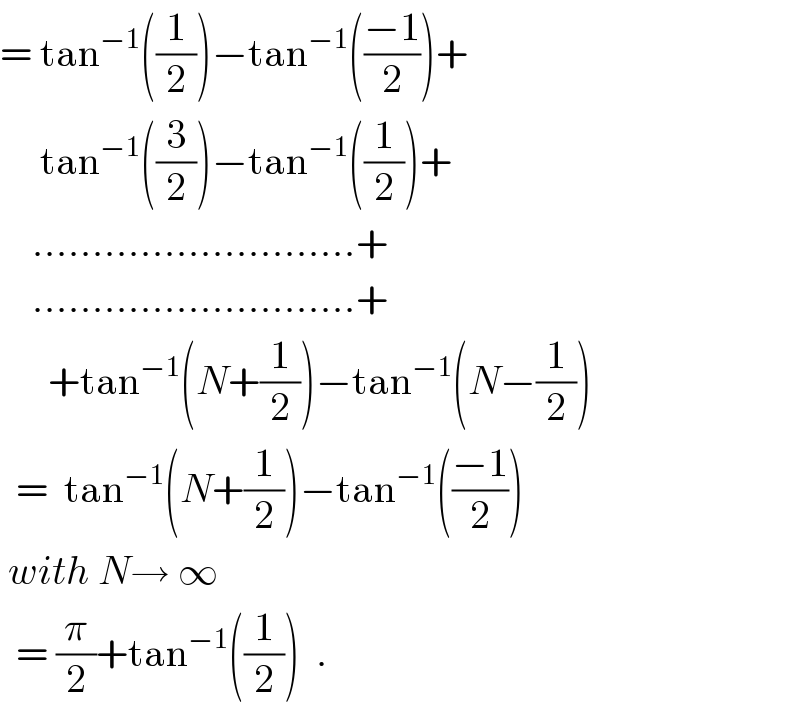
= tan^(−1) ((1/2))−tan^(−1) (((−1)/2))+ tan^(−1) ((3/2))−tan^(−1) ((1/2))+ ...........................+ ...........................+ +tan^(−1) (N+(1/2))−tan^(−1) (N−(1/2)) = tan^(−1) (N+(1/2))−tan^(−1) (((−1)/2)) with N→ ∞ = (π/2)+tan^(−1) ((1/2)) .
$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\right)+ \\ $$$$\:\:\:\:\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+ \\ $$$$\:\:\:\:………………………+ \\ $$$$\:\:\:\:………………………+ \\ $$$$\:\:\:\:\:\:+\mathrm{tan}^{−\mathrm{1}} \left({N}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{tan}^{−\mathrm{1}} \left({N}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:=\:\:\mathrm{tan}^{−\mathrm{1}} \left({N}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:{with}\:{N}\rightarrow\:\infty \\ $$$$\:\:=\:\frac{\pi}{\mathrm{2}}+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *