Menu Close

n-1-1-1-2-1-3-1-n-n-1-n-2-

Tinku Tara 0 Comments
Pin




Question Number 146735 by qaz last updated on 15/Jul/21
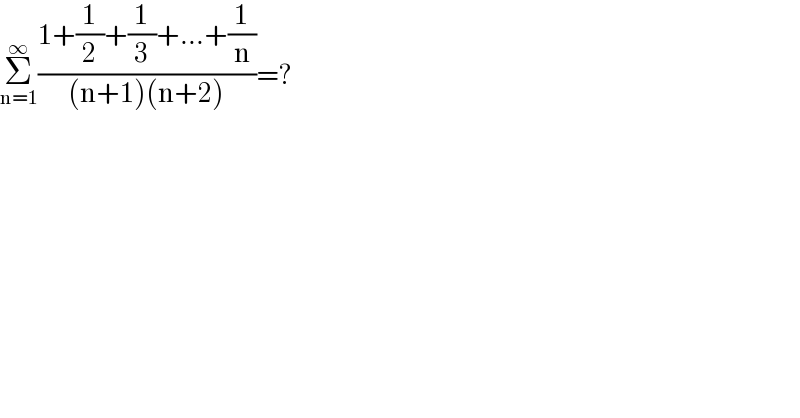
Σ_(n=1) ^∞ ((1+(1/2)+(1/3)+...+(1/n))/((n+1)(n+2)))=?
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{n}}}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}=? \\ $$
Answered by Olaf_Thorendsen last updated on 15/Jul/21
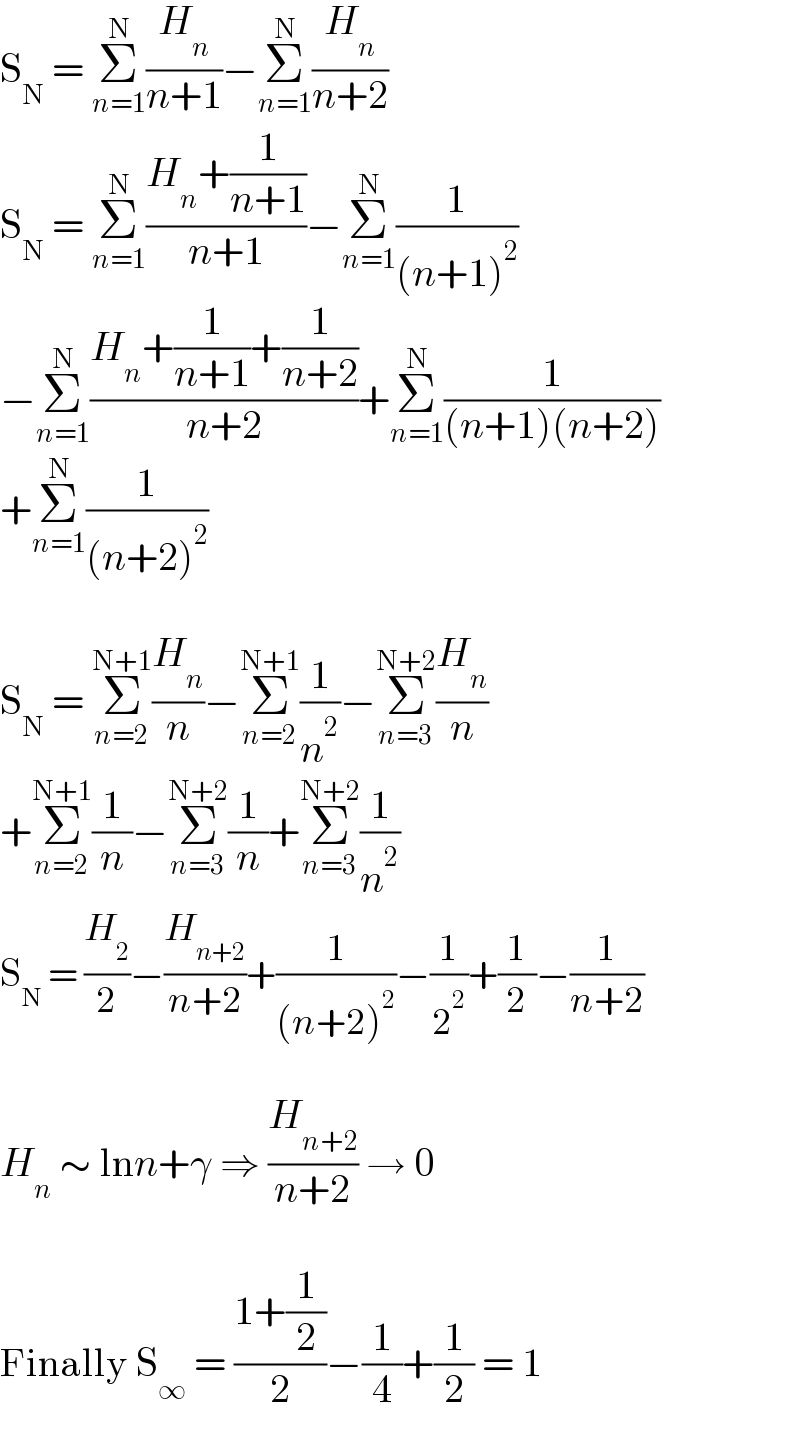
S_N = Σ_(n=1) ^N (H_n /(n+1))−Σ_(n=1) ^N (H_n /(n+2)) S_N = Σ_(n=1) ^N ((H_n +(1/(n+1)))/(n+1))−Σ_(n=1) ^N (1/((n+1)^2 )) −Σ_(n=1) ^N ((H_n +(1/(n+1))+(1/(n+2)))/(n+2))+Σ_(n=1) ^N (1/((n+1)(n+2))) +Σ_(n=1) ^N (1/((n+2)^2 )) S_N = Σ_(n=2) ^(N+1) (H_n /n)−Σ_(n=2) ^(N+1) (1/n^2 )−Σ_(n=3) ^(N+2) (H_n /n) +Σ_(n=2) ^(N+1) (1/n)−Σ_(n=3) ^(N+2) (1/n)+Σ_(n=3) ^(N+2) (1/n^2 ) S_N = (H_2 /2)−(H_(n+2) /(n+2))+(1/((n+2)^2 ))−(1/2^2 )+(1/2)−(1/(n+2)) H_n ∼ lnn+γ ⇒ (H_(n+2) /(n+2)) → 0 Finally S_∞ = ((1+(1/2))/2)−(1/4)+(1/2) = 1
$$\mathrm{S}_{\mathrm{N}} \:=\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{{H}_{{n}} }{{n}+\mathrm{1}}−\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{{H}_{{n}} }{{n}+\mathrm{2}} \\ $$$$\mathrm{S}_{\mathrm{N}} \:=\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{{H}_{{n}} +\frac{\mathrm{1}}{{n}+\mathrm{1}}}{{n}+\mathrm{1}}−\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$−\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{{H}_{{n}} +\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}}{{n}+\mathrm{2}}+\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$+\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{S}_{\mathrm{N}} \:=\:\underset{{n}=\mathrm{2}} {\overset{\mathrm{N}+\mathrm{1}} {\sum}}\frac{{H}_{{n}} }{{n}}−\underset{{n}=\mathrm{2}} {\overset{\mathrm{N}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\underset{{n}=\mathrm{3}} {\overset{\mathrm{N}+\mathrm{2}} {\sum}}\frac{{H}_{{n}} }{{n}} \\ $$$$+\underset{{n}=\mathrm{2}} {\overset{\mathrm{N}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{n}}−\underset{{n}=\mathrm{3}} {\overset{\mathrm{N}+\mathrm{2}} {\sum}}\frac{\mathrm{1}}{{n}}+\underset{{n}=\mathrm{3}} {\overset{\mathrm{N}+\mathrm{2}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$\mathrm{S}_{\mathrm{N}} \:=\:\frac{{H}_{\mathrm{2}} }{\mathrm{2}}−\frac{{H}_{{n}+\mathrm{2}} }{{n}+\mathrm{2}}+\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}} \\ $$$$ \\ $$$${H}_{{n}} \:\sim\:\mathrm{ln}{n}+\gamma\:\Rightarrow\:\frac{{H}_{{n}+\mathrm{2}} }{{n}+\mathrm{2}}\:\rightarrow\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Finally}\:\mathrm{S}_{\infty} \:=\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{1} \\ $$
Answered by mnjuly1970 last updated on 15/Jul/21
solution.. we know that: Σ_(n≥1) ((H_n x^( n+1) )/(n+1)) = (1/2) log^( 2) (1−x ) Σ_(n≥1) (H_n /((n+1)(n+2))) =(1/2) ∫_0 ^( 1) log^2 (x)dx = (1/2) {[xlog^( 2) (x)]_0 ^( 1) −2 ∫_0 ^( 1) log(x)dx} = −∫_0 ^( 1) log(x)dx =1....✓
$$\:\:\:{solution}.. \\ $$$$\:\:\:{we}\:{know}\:{that}: \\ $$$$\:\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{H}_{{n}} {x}^{\:{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:{log}^{\:\mathrm{2}} \left(\mathrm{1}−{x}\:\right) \\ $$$$\:\:\:\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{H}_{{n}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {log}^{\mathrm{2}} \left({x}\right){dx} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\left[{xlog}^{\:\mathrm{2}} \left({x}\right)\right]_{\mathrm{0}} ^{\:\mathrm{1}} −\mathrm{2}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {log}\left({x}\right){dx}\right\} \\ $$$$\:\:\:\:\:\:\:=\:−\int_{\mathrm{0}} ^{\:\mathrm{1}} {log}\left({x}\right){dx}\:=\mathrm{1}….\checkmark \\ $$$$\:\: \\ $$$$\:\:\:\:\: \\ $$
Commented by qaz last updated on 15/Jul/21
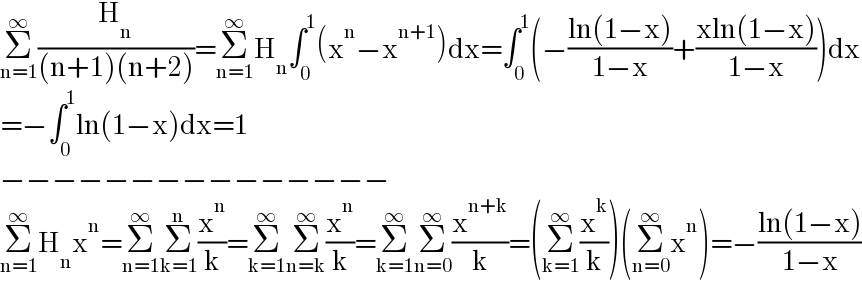
Σ_(n=1) ^∞ (H_n /((n+1)(n+2)))=Σ_(n=1) ^∞ H_n ∫_0 ^1 (x^n −x^(n+1) )dx=∫_0 ^1 (−((ln(1−x))/(1−x))+((xln(1−x))/(1−x)))dx =−∫_0 ^1 ln(1−x)dx=1 −−−−−−−−−−−−−−− Σ_(n=1) ^∞ H_n x^n =Σ_(n=1) ^∞ Σ_(k=1) ^n (x^n /k)=Σ_(k=1) ^∞ Σ_(n=k) ^∞ (x^n /k)=Σ_(k=1) ^∞ Σ_(n=0) ^∞ (x^(n+k) /k)=(Σ_(k=1) ^∞ (x^k /k))(Σ_(n=0) ^∞ x^n )=−((ln(1−x))/(1−x))
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{H}_{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{H}_{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{\mathrm{n}+\mathrm{1}} \right)\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}}+\frac{\mathrm{xln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}}\right)\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}=\mathrm{1} \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{H}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} =\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{k}}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{k}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{k}}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}+\mathrm{k}} }{\mathrm{k}}=\left(\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{k}} }{\mathrm{k}}\right)\left(\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{x}^{\mathrm{n}} \right)=−\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *