Question Number 98112 by M±th+et+s last updated on 11/Jun/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}^{\mathrm{2}} } } \\ $$
Answered by maths mind last updated on 11/Jun/20
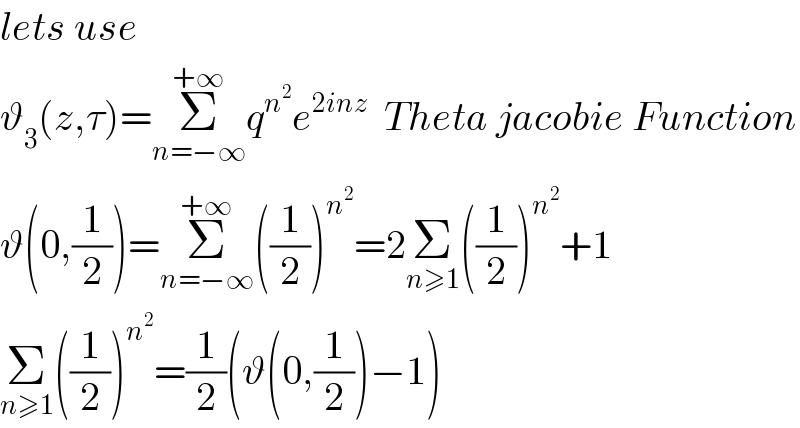
$${lets}\:{use} \\ $$$$\vartheta_{\mathrm{3}} \left({z},\tau\right)=\underset{{n}=−\infty} {\overset{+\infty} {\sum}}{q}^{{n}^{\mathrm{2}} } {e}^{\mathrm{2}{inz}} \:\:{Theta}\:{jacobie}\:{Function} \\ $$$$\vartheta\left(\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right)=\underset{{n}=−\infty} {\overset{+\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}^{\mathrm{2}} } =\mathrm{2}\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}^{\mathrm{2}} } +\mathrm{1} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}^{\mathrm{2}} } =\frac{\mathrm{1}}{\mathrm{2}}\left(\vartheta\left(\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}\right) \\ $$
Commented by M±th+et+s last updated on 11/Jun/20
$${thank}\:{you}\:{sir}\:{well}\:{done} \\ $$
