Question Number 127080 by Dwaipayan Shikari last updated on 26/Dec/20
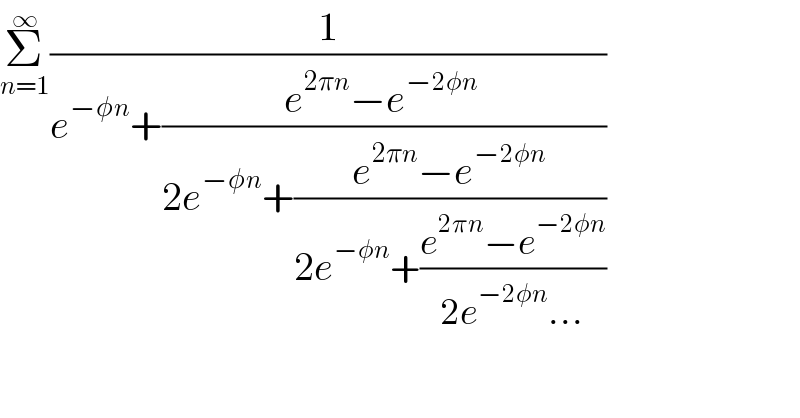
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{e}^{−\phi{n}} +\frac{{e}^{\mathrm{2}\pi{n}} −{e}^{−\mathrm{2}\phi{n}} \:}{\mathrm{2}{e}^{−\phi{n}} +\frac{{e}^{\mathrm{2}\pi{n}} −{e}^{−\mathrm{2}\phi{n}} }{\mathrm{2}{e}^{−\phi{n}} +\frac{{e}^{\mathrm{2}\pi{n}} −{e}^{−\mathrm{2}\phi{n}} }{\mathrm{2}{e}^{−\mathrm{2}\phi{n}} …}}}} \\ $$
Commented by Dwaipayan Shikari last updated on 26/Dec/20
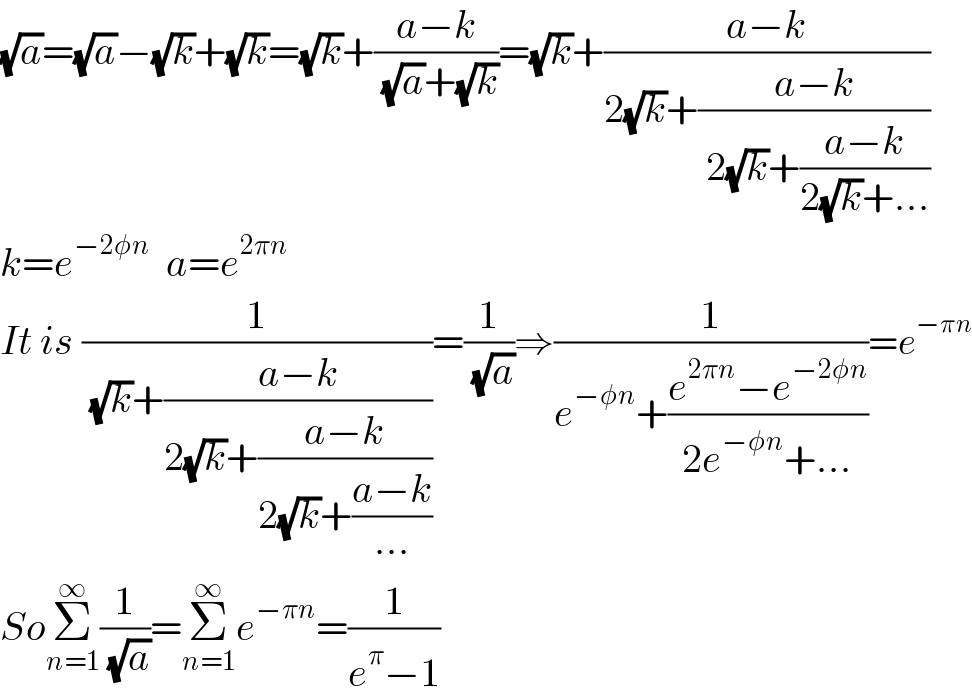
$$\sqrt{{a}}=\sqrt{{a}}−\sqrt{{k}}+\sqrt{{k}}=\sqrt{{k}}+\frac{{a}−{k}}{\:\sqrt{{a}}+\sqrt{{k}}}=\sqrt{{k}}+\frac{{a}−{k}}{\mathrm{2}\sqrt{{k}}+\frac{{a}−{k}}{\:\mathrm{2}\sqrt{{k}}+\frac{{a}−{k}}{\mathrm{2}\sqrt{{k}}+…}}} \\ $$$${k}={e}^{−\mathrm{2}\phi{n}} \:\:{a}={e}^{\mathrm{2}\pi{n}} \\ $$$${It}\:{is}\:\frac{\mathrm{1}}{\:\sqrt{{k}}+\frac{{a}−{k}}{\mathrm{2}\sqrt{{k}}+\frac{{a}−{k}}{\mathrm{2}\sqrt{{k}}+\frac{{a}−{k}}{…}}}}=\frac{\mathrm{1}}{\:\sqrt{{a}}}\Rightarrow\frac{\mathrm{1}}{{e}^{−\phi{n}} +\frac{{e}^{\mathrm{2}\pi{n}} −{e}^{−\mathrm{2}\phi{n}} }{\mathrm{2}{e}^{−\phi{n}} +…}}={e}^{−\pi{n}} \\ $$$${So}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{a}}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{e}^{−\pi{n}} =\frac{\mathrm{1}}{{e}^{\pi} −\mathrm{1}} \\ $$
