Question Number 32755 by 7991 last updated on 01/Apr/18
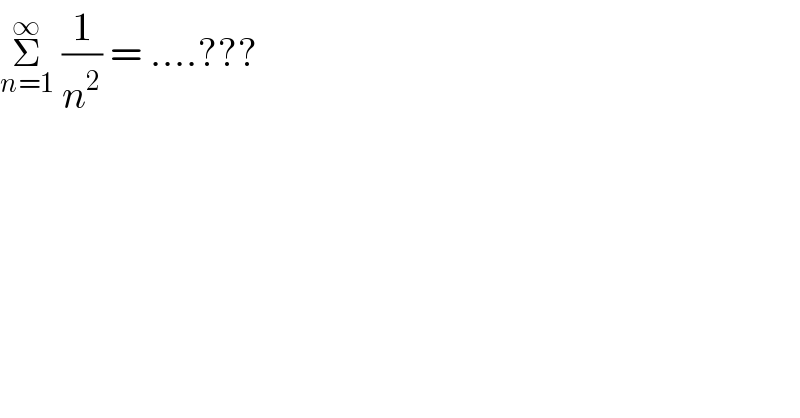
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\:….??? \\ $$
Commented by Rio Mike last updated on 01/Apr/18
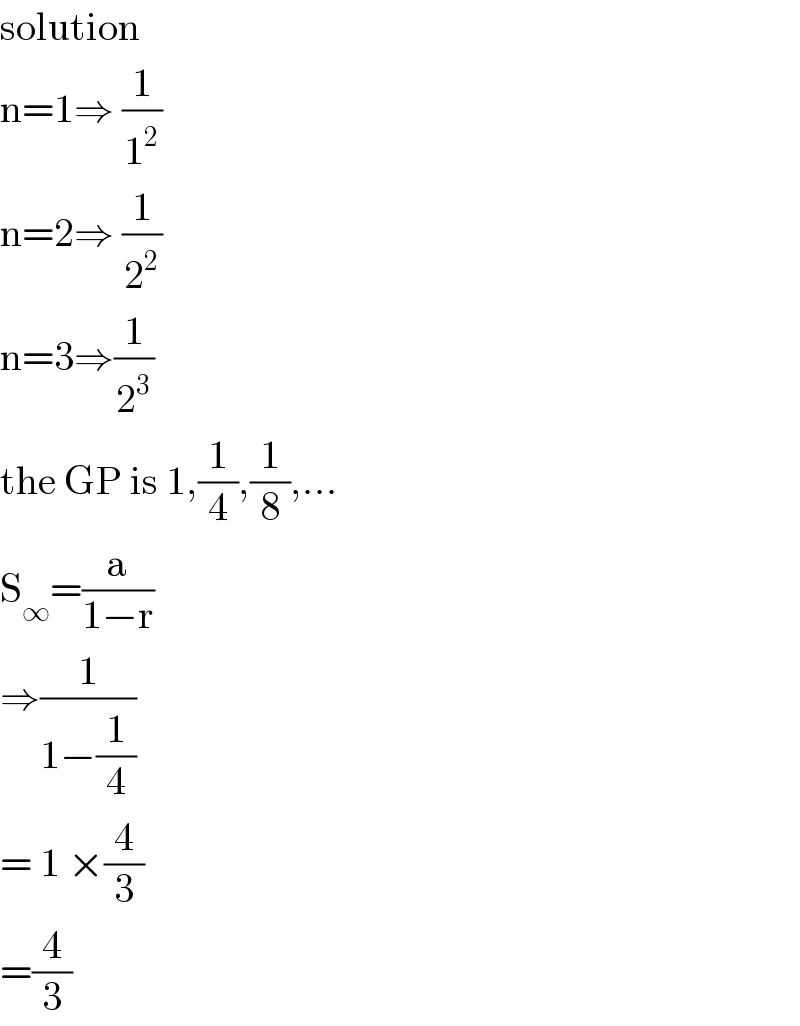
$$\mathrm{solution} \\ $$$$\mathrm{n}=\mathrm{1}\Rightarrow\:\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} } \\ $$$$\mathrm{n}=\mathrm{2}\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} } \\ $$$$\mathrm{n}=\mathrm{3}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} } \\ $$$$\mathrm{the}\:\mathrm{GP}\:\mathrm{is}\:\mathrm{1},\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{8}},… \\ $$$$\mathrm{S}_{\infty} =\frac{\mathrm{a}}{\mathrm{1}−\mathrm{r}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\:\mathrm{1}\:×\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by abdo imad last updated on 01/Apr/18
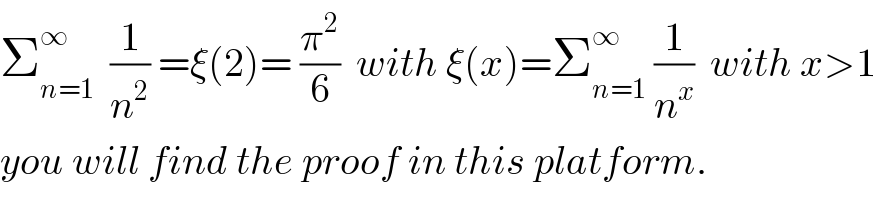
$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\xi\left(\mathrm{2}\right)=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:{with}\:\xi\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{{x}} }\:\:{with}\:{x}>\mathrm{1}\: \\ $$$${you}\:{will}\:{find}\:{the}\:{proof}\:{in}\:{this}\:{platform}. \\ $$
Commented by abdo imad last updated on 01/Apr/18
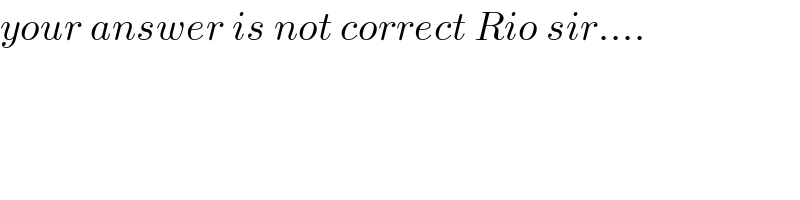
$${your}\:{answer}\:{is}\:{not}\:{correct}\:{Rio}\:{sir}…. \\ $$
Commented by JDamian last updated on 05/Apr/18
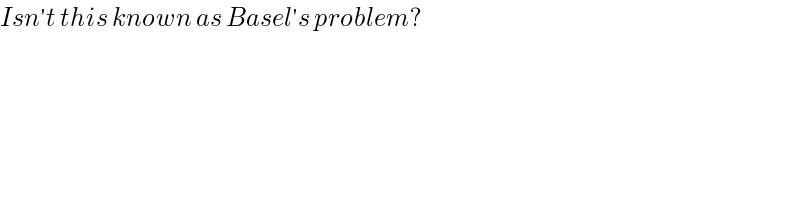
$${Isn}'{t}\:{this}\:{known}\:{as}\:{Basel}'{s}\:{problem}? \\ $$
Commented by Rasheed.Sindhi last updated on 05/Apr/18

$$\mathrm{1},\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{8}},…\:\mathrm{is}\:\mathrm{not}\:\mathrm{GP} \\ $$$$\because\:\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{\div}\mathrm{1}\neq\frac{\mathrm{1}}{\mathrm{8}}\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\neq\frac{\mathrm{1}}{\mathrm{2}} \\ $$
