Question Number 93509 by Shakhzod last updated on 13/May/20
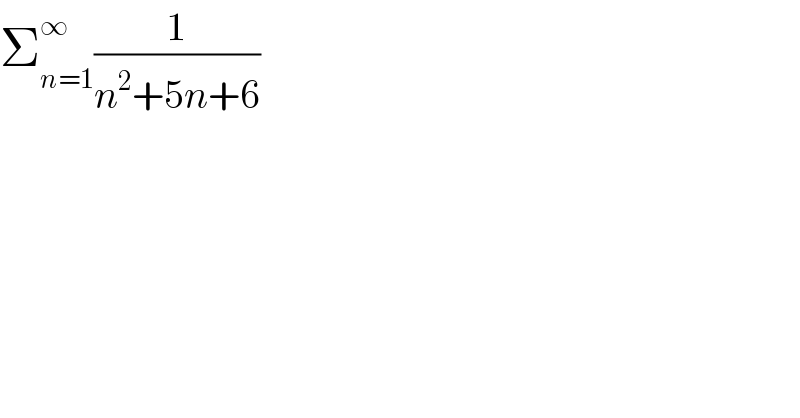
$$\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{5}{n}+\mathrm{6}}\: \\ $$
Commented by Shakhzod last updated on 13/May/20
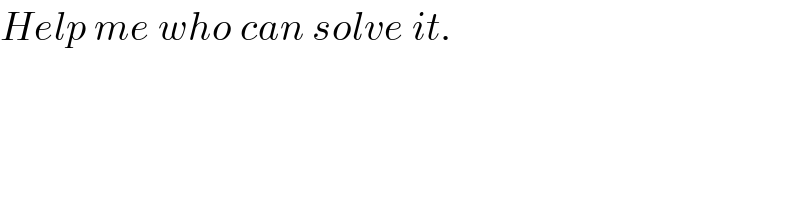
$${Help}\:{me}\:{who}\:{can}\:{solve}\:{it}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 13/May/20
![Σ_(n=1) ^∞ (1/((n+2)(n+3))) = Σ_(n=1) ^∞ [(1/(n+2))−(1/(n+3))] =Σ_(n=1) ^∞ [(1/n)−(1/(n+1))] −(2/3)= {lim_(n→∞) [1−(1/(n+1))]}−(2/3) =(1/3)](https://www.tinkutara.com/question/Q93525.png)
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{3}\right)}\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{3}}\right] \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right]\:−\frac{\mathrm{2}}{\mathrm{3}}=\:\left\{\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right]\right\}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 13/May/20
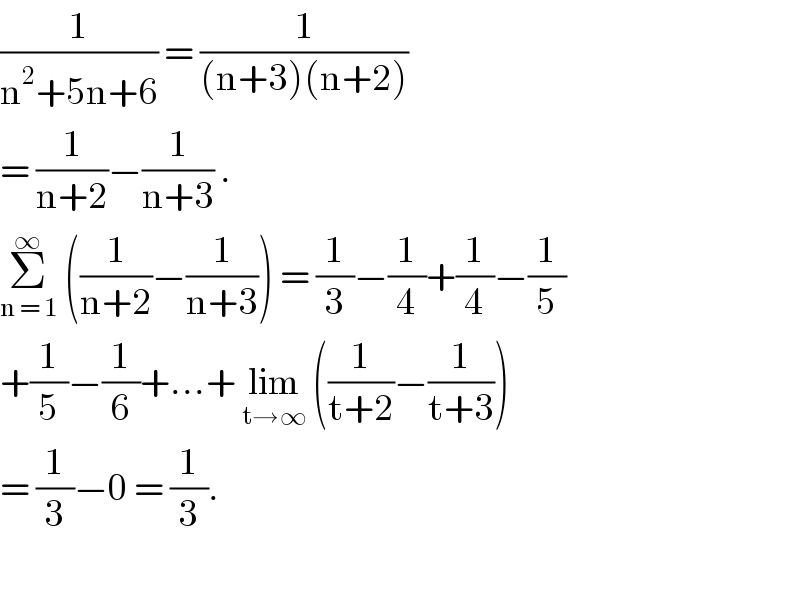
$$\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} +\mathrm{5n}+\mathrm{6}}\:=\:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{2}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{3}}\:. \\ $$$$\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{3}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}}+…+\:\underset{\mathrm{t}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{t}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{3}}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{0}\:=\:\frac{\mathrm{1}}{\mathrm{3}}.\: \\ $$$$ \\ $$
Commented by Shakhzod last updated on 13/May/20
$${Thank}\:{you}\:{so}\:{much}. \\ $$
Commented by Shakhzod last updated on 13/May/20
$${Thank}\:{youfriend}. \\ $$
