n-1-1-n-2-k-2-

Question Number 128806 by LUFFY last updated on 10/Jan/21

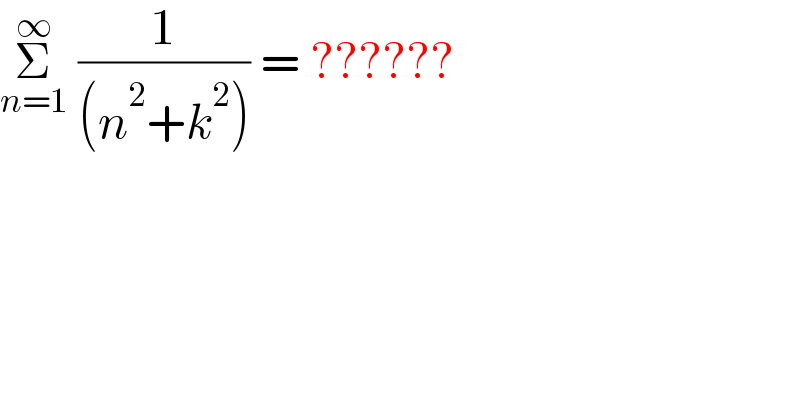
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +{k}^{\mathrm{2}} \right)}\:=\:?????? \\ $$

Answered by Dwaipayan Shikari last updated on 10/Jan/21

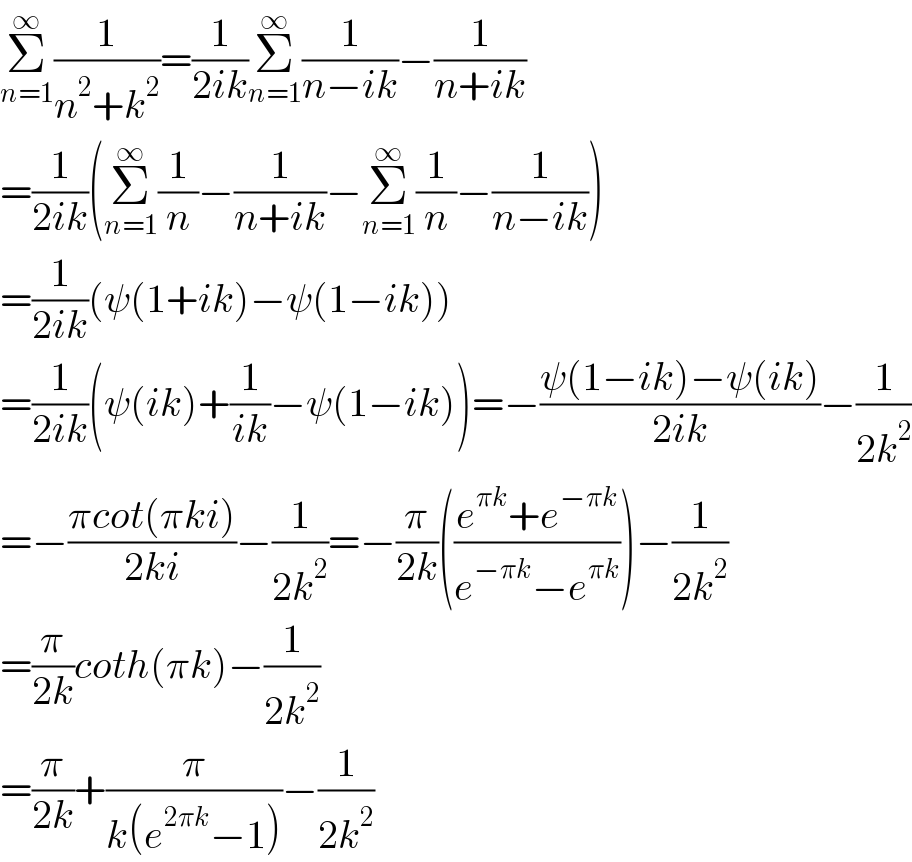
Σ_(n=1) ^∞ (1/(n^2 +k^2 ))=(1/(2ik))Σ_(n=1) ^∞ (1/(n−ik))−(1/(n+ik)) =(1/(2ik))(Σ_(n=1) ^∞ (1/n)−(1/(n+ik))−Σ_(n=1) ^∞ (1/n)−(1/(n−ik))) =(1/(2ik))(ψ(1+ik)−ψ(1−ik)) =(1/(2ik))(ψ(ik)+(1/(ik))−ψ(1−ik))=−((ψ(1−ik)−ψ(ik))/(2ik))−(1/(2k^2 )) =−((πcot(πki))/(2ki))−(1/(2k^2 ))=−(π/(2k))(((e^(πk) +e^(−πk) )/(e^(−πk) −e^(πk) )))−(1/(2k^2 )) =(π/(2k))coth(πk)−(1/(2k^2 )) =(π/(2k))+(π/(k(e^(2πk) −1)))−(1/(2k^2 ))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{k}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{ik}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}−{ik}}−\frac{\mathrm{1}}{{n}+{ik}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ik}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+{ik}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}−{ik}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ik}}\left(\psi\left(\mathrm{1}+{ik}\right)−\psi\left(\mathrm{1}−{ik}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ik}}\left(\psi\left({ik}\right)+\frac{\mathrm{1}}{{ik}}−\psi\left(\mathrm{1}−{ik}\right)\right)=−\frac{\psi\left(\mathrm{1}−{ik}\right)−\psi\left({ik}\right)}{\mathrm{2}{ik}}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} } \\ $$$$=−\frac{\pi{cot}\left(\pi{ki}\right)}{\mathrm{2}{ki}}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }=−\frac{\pi}{\mathrm{2}{k}}\left(\frac{{e}^{\pi{k}} +{e}^{−\pi{k}} }{{e}^{−\pi{k}} −{e}^{\pi{k}} }\right)−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2}{k}}{coth}\left(\pi{k}\right)−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2}{k}}+\frac{\pi}{{k}\left({e}^{\mathrm{2}\pi{k}} −\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} } \\ $$

Answered by Olaf last updated on 10/Jan/21

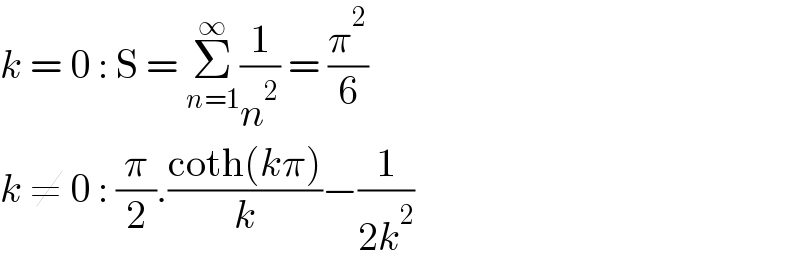
k = 0 : S = Σ_(n=1) ^∞ (1/n^2 ) = (π^2 /6) k ≠ 0 : (π/2).((coth(kπ))/k)−(1/(2k^2 ))

$${k}\:=\:\mathrm{0}\::\:\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$${k}\:\neq\:\mathrm{0}\::\:\frac{\pi}{\mathrm{2}}.\frac{\mathrm{coth}\left({k}\pi\right)}{{k}}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} } \\ $$

Commented by Dwaipayan Shikari last updated on 10/Jan/21

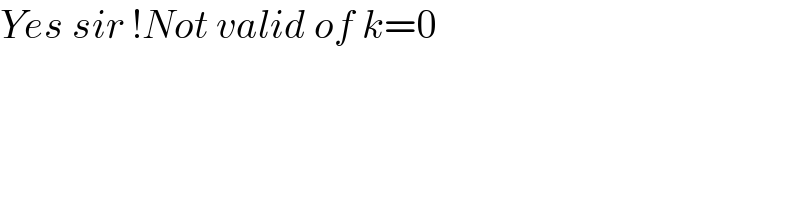
$${Yes}\:{sir}\:!{Not}\:{valid}\:{of}\:{k}=\mathrm{0} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply