Question Number 182794 by mnjuly1970 last updated on 14/Dec/22
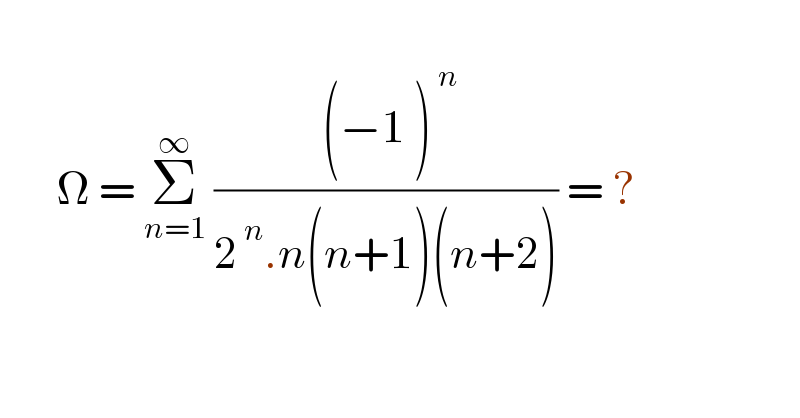
$$ \\ $$$$\:\:\:\:\:\:\:\Omega\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\:\left(−\underset{} {\overset{} {\mathrm{1}}}\:\right)^{\:{n}} }{\mathrm{2}^{\:{n}} .{n}\left({n}\underset{} {\overset{} {+}}\mathrm{1}\right)\left({n}\underset{} {\overset{} {+}}\mathrm{2}\right)}\:=\:?\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
Answered by ARUNG_Brandon_MBU last updated on 14/Dec/22
![S(x)=Σ_(n=1) ^∞ (x^(n+2) /(n(n+1)(n+2))) ⇒S ′(x)=Σ_(n=1) ^∞ (x^(n+1) /(n(n+1))) ⇒S ′′(x)=Σ_(n=1) ^∞ (x^n /n) ⇒S ′′′(x)=Σ_(n=1) ^∞ x^(n−1) =(1/(1−x)) ⇒S ′′(x)=Σ_(n=1) ^∞ (x^n /n)=−ln(1−x)+C_1 , C_1 =0 ⇒S ′(x)=Σ_(n=1) ^∞ (x^(n+1) /(n(n+1)))=(1−x)ln(1−x)+x−1+C_2 , C_2 =1 ⇒S ′(x)=ln(1−x)−xln(1−x)+x ⇒S(x)=∫[−xln(1−x)+ln(1−x)+x]dx ⇒S(x)=−(x^2 /2)ln(1−x)+(1/2)((x^2 /2)+x+ln∣x−1∣) +(1−x)−(1−x)ln(1−x)+(x^2 /2)+C_3 , C_3 =−1 ⇒Σ_(n=1) ^∞ (((−1)^n )/(2^n n(n+1)(n+2)))=2^2 S(−(1/2)) =−(1/2)ln((3/2))+2((1/8)−(1/2)+ln((3/2)))+6−6ln((3/2))+(1/2)−4 ⇒Ω=(7/4)−(9/2)ln((3/2))](https://www.tinkutara.com/question/Q182801.png)
$${S}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}+\mathrm{2}} }{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:\Rightarrow{S}\:'\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}+\mathrm{1}} }{{n}\left({n}+\mathrm{1}\right)} \\ $$$$\Rightarrow{S}\:''\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}\:\Rightarrow{S}\:'''\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\Rightarrow{S}\:''\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}=−\mathrm{ln}\left(\mathrm{1}−{x}\right)+{C}_{\mathrm{1}} ,\:{C}_{\mathrm{1}} =\mathrm{0} \\ $$$$\Rightarrow{S}\:'\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}+\mathrm{1}} }{{n}\left({n}+\mathrm{1}\right)}=\left(\mathrm{1}−{x}\right)\mathrm{ln}\left(\mathrm{1}−{x}\right)+{x}−\mathrm{1}+{C}_{\mathrm{2}} ,\:{C}_{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{S}\:'\left({x}\right)=\mathrm{ln}\left(\mathrm{1}−{x}\right)−{x}\mathrm{ln}\left(\mathrm{1}−{x}\right)+{x} \\ $$$$\Rightarrow{S}\left({x}\right)=\int\left[−{x}\mathrm{ln}\left(\mathrm{1}−{x}\right)+\mathrm{ln}\left(\mathrm{1}−{x}\right)+{x}\right]{dx} \\ $$$$\Rightarrow{S}\left({x}\right)=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}−{x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{x}+\mathrm{ln}\mid{x}−\mathrm{1}\mid\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{1}−{x}\right)−\left(\mathrm{1}−{x}\right)\mathrm{ln}\left(\mathrm{1}−{x}\right)+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{C}_{\mathrm{3}} ,\:{C}_{\mathrm{3}} =−\mathrm{1} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} {n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}=\mathrm{2}^{\mathrm{2}} {S}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right)+\mathrm{6}−\mathrm{6ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{4} \\ $$$$\Rightarrow\Omega=\frac{\mathrm{7}}{\mathrm{4}}−\frac{\mathrm{9}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by mnjuly1970 last updated on 14/Dec/22
$${grateful}.{thank}\:{you}\:{sir}\: \\ $$
