Question Number 150059 by mathdanisur last updated on 09/Aug/21

$$\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}\centerdot\left(\mathrm{2n}\:+\:\mathrm{1}\right)}\:=\:? \\ $$
Answered by Kamel last updated on 09/Aug/21
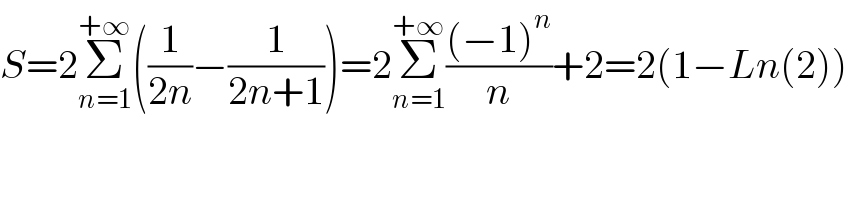
$${S}=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}+\mathrm{2}=\mathrm{2}\left(\mathrm{1}−{Ln}\left(\mathrm{2}\right)\right) \\ $$
Commented by mathdanisur last updated on 09/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Answered by Ar Brandon last updated on 09/Aug/21

$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{2}}}\right)=\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\psi\left(\mathrm{1}\right) \\ $$$$\:\:\:=\mathrm{2}+\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\mathrm{1}\right)=\mathrm{2}−\gamma−\mathrm{2ln2}+\gamma=\mathrm{2}−\mathrm{ln4} \\ $$
Commented by Ar Brandon last updated on 09/Aug/21

$$\psi\left(\mathrm{x}\right)=−\gamma+\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{x}}\right)\:=\:\frac{\Gamma'\left(\mathrm{x}\right)}{\Gamma\left(\mathrm{x}\right)} \\ $$$$\psi\left(\mathrm{x}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{x}}+\psi\left(\mathrm{x}\right)\:,\:\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\gamma−\mathrm{2ln2} \\ $$$$\psi\left(\frac{\mathrm{r}}{\mathrm{m}}\right)=−\gamma−\mathrm{ln}\left(\mathrm{2m}\right)−\frac{\pi}{\mathrm{2}}\mathrm{cot}\left(\frac{\mathrm{r}\pi}{\mathrm{m}}\right)+\mathrm{2}\underset{\mathrm{n}=\mathrm{1}} {\overset{\mid\frac{\mathrm{m}−\mathrm{1}}{\mathrm{2}}\mid} {\sum}}\mathrm{cos}\left(\frac{\mathrm{2}\pi\mathrm{nr}}{\mathrm{m}}\right)\mathrm{ln}\:\mathrm{sin}\left(\frac{\pi\mathrm{n}}{\mathrm{m}}\right) \\ $$$$\psi\left({z}+\mathrm{1}\right)=−\gamma+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\zeta\left({n}\right){z}^{{n}−\mathrm{1}} \\ $$$$\psi\left(\mathrm{x}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\mathrm{t}^{\mathrm{x}−\mathrm{1}} }{\mathrm{1}−\mathrm{t}}\mathrm{dt} \\ $$$$\psi'\left(\mathrm{x}\right)=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{x}−\mathrm{1}} \mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}−\mathrm{t}}\mathrm{dt} \\ $$$$\psi\left(\mathrm{x}\right)−\psi\left(\mathrm{1}−\mathrm{x}\right)=−\pi\mathrm{cot}\left(\pi\mathrm{x}\right) \\ $$$$\psi^{\left(\mathrm{1}\right)} \left(\mathrm{x}\right)+\psi^{\left(\mathrm{1}\right)} \left(\mathrm{1}−\mathrm{x}\right)=\pi^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cot}^{\mathrm{2}} \left(\pi\mathrm{x}\right)\right) \\ $$$$\psi^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)−\psi^{\left(\mathrm{2}\right)} \left(\mathrm{1}−\mathrm{x}\right)=−\mathrm{2}\pi^{\mathrm{3}} \left(\mathrm{1}+\mathrm{cot}^{\mathrm{2}} \left(\pi\mathrm{x}\right)\right)\mathrm{cot}\left(\pi\mathrm{x}\right) \\ $$
Commented by mathdanisur last updated on 09/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Commented by Tawa11 last updated on 09/Aug/21

$$\mathrm{weldone}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 09/Aug/21

$$\mathrm{sir}\:\mathrm{Ar}\:\mathrm{brandon},\:\mathrm{please}\:\mathrm{give}\:\mathrm{me}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of}\:\:\:\psi\:\:\mathrm{that}\:\mathrm{you}\:\mathrm{used}. \\ $$$$\mathrm{or}\:\mathrm{books}\:\mathrm{sir}.\:\mathrm{please}\:… \\ $$
Commented by mnjuly1970 last updated on 09/Aug/21
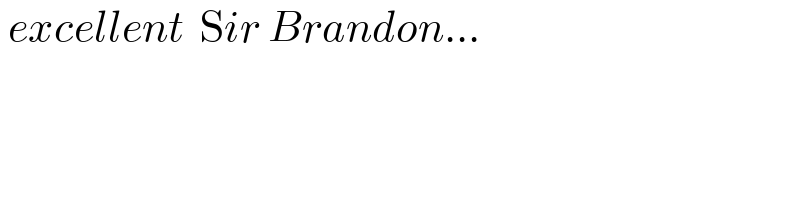
$$\:{excellent}\:\:\mathrm{S}{ir}\:{Brandon}… \\ $$
Commented by Ar Brandon last updated on 09/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}\:! \\ $$
Commented by Ar Brandon last updated on 09/Aug/21

$$\mathrm{They}\:\mathrm{are}\:\mathrm{part}\:\mathrm{of}\:\mathrm{your}\:\mathrm{teachings} \\ $$😃
Commented by Tawa11 last updated on 09/Aug/21

$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
Commented by Ar Brandon last updated on 09/Aug/21
My pleasure
