n-1-1-n-H-2n-2n-

Question Number 158691 by mnjuly1970 last updated on 07/Nov/21

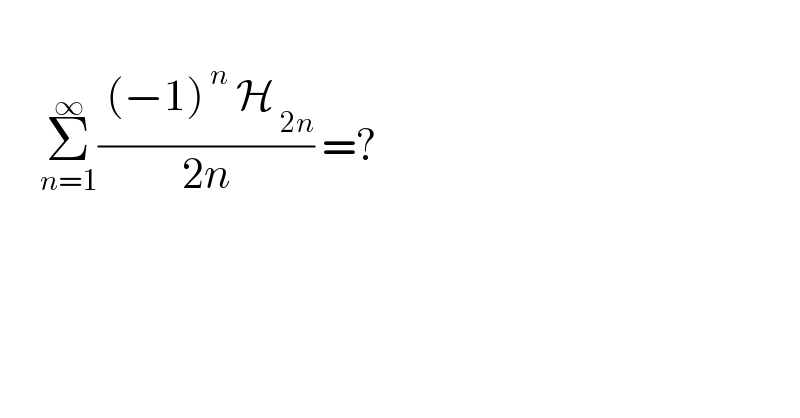
Σ_(n=1) ^∞ (( (−1)^( n) H_( 2n) )/(2n)) =?

$$ \\ $$$$\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\left(−\mathrm{1}\right)^{\:{n}} \:\mathcal{H}_{\:\mathrm{2}{n}} }{\mathrm{2}{n}}\:=? \\ $$

Answered by qaz last updated on 08/Nov/21

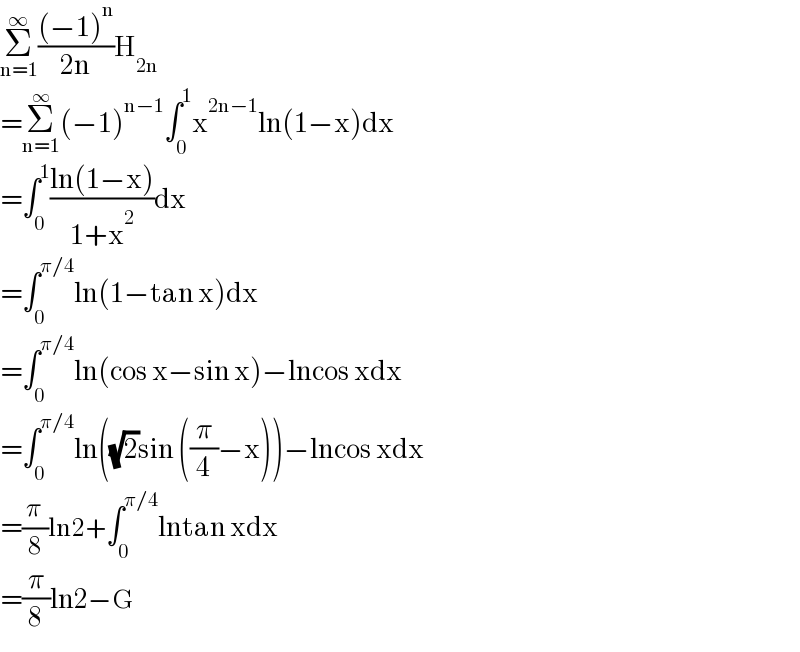
Σ_(n=1) ^∞ (((−1)^n )/(2n))H_(2n) =Σ_(n=1) ^∞ (−1)^(n−1) ∫_0 ^1 x^(2n−1) ln(1−x)dx =∫_0 ^1 ((ln(1−x))/(1+x^2 ))dx =∫_0 ^(π/4) ln(1−tan x)dx =∫_0 ^(π/4) ln(cos x−sin x)−lncos xdx =∫_0 ^(π/4) ln((√2)sin ((π/4)−x))−lncos xdx =(π/8)ln2+∫_0 ^(π/4) lntan xdx =(π/8)ln2−G

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}}\mathrm{H}_{\mathrm{2n}} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{2n}−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{ln}\left(\mathrm{1}−\mathrm{tan}\:\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)−\mathrm{lncos}\:\mathrm{xdx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{ln}\left(\sqrt{\mathrm{2}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\right)−\mathrm{lncos}\:\mathrm{xdx} \\ $$$$=\frac{\pi}{\mathrm{8}}\mathrm{ln2}+\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{lntan}\:\mathrm{xdx} \\ $$$$=\frac{\pi}{\mathrm{8}}\mathrm{ln2}−\mathrm{G} \\ $$

Commented by mnjuly1970 last updated on 08/Nov/21

$${very}\:{nice}\:{sir}\:{qaz} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply