Question Number 145951 by ArielVyny last updated on 09/Jul/21

$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}=?? \\ $$
Answered by Olaf_Thorendsen last updated on 09/Jul/21
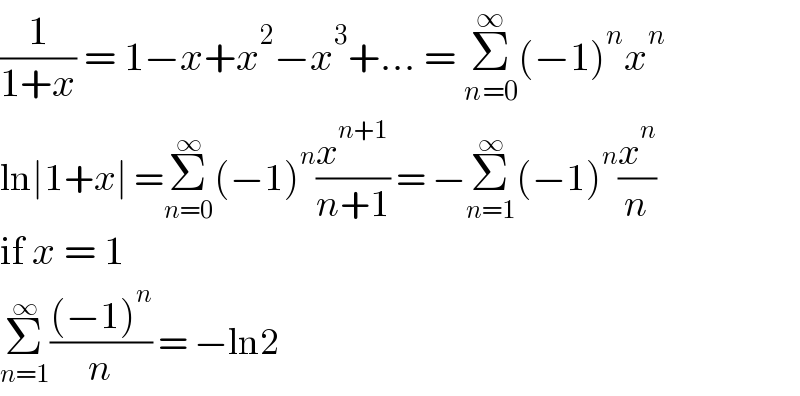
$$\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\:\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +…\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \\ $$$$\mathrm{ln}\mid\mathrm{1}+{x}\mid\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{{n}} }{{n}} \\ $$$$\mathrm{if}\:{x}\:=\:\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:=\:−\mathrm{ln2} \\ $$
