Question Number 108298 by bachamohamed last updated on 16/Aug/20
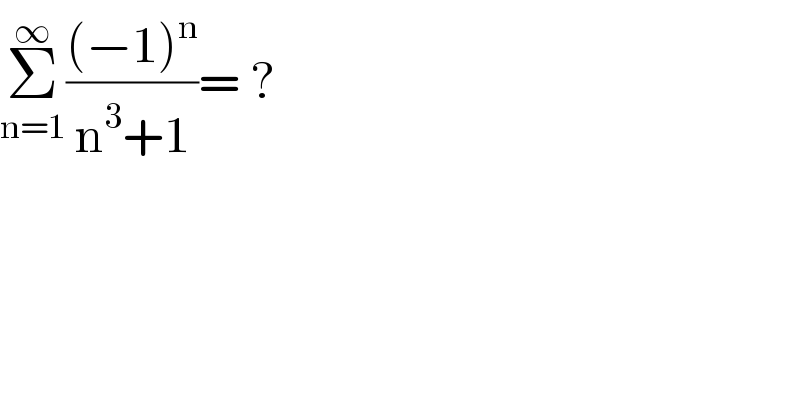
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{3}} +\mathrm{1}}=\:? \\ $$
Answered by Dwaipayan Shikari last updated on 16/Aug/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .\left(\frac{{A}}{{n}+\mathrm{1}}+\frac{{Bn}+{C}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{{n}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}+\frac{\mathrm{2}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}+\mathrm{1}}−\overset{\infty} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{{n}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}+\overset{\infty} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{2}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}\right) \\ $$$$\overset{\infty} {\sum}\left(−\mathrm{1}\right)^{{n}} .\frac{\mathrm{1}}{{n}+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{7}}−…={log}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$$\overset{\infty} {\sum}\left(−\mathrm{1}\right)^{{n}} .\frac{\mathrm{2}−{n}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}=\overset{\infty} {\sum}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} .\frac{{n}−\mathrm{2}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}=−\mathrm{1}+\mathrm{0}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{2}}{\mathrm{13}}−\frac{\mathrm{3}}{\mathrm{21}}+.. \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+….=\frac{\pi}{\mathrm{4}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{7}}+…=\frac{\pi}{\mathrm{4}}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$….. \\ $$$$ \\ $$
