Question Number 114758 by bobhans last updated on 21/Sep/20
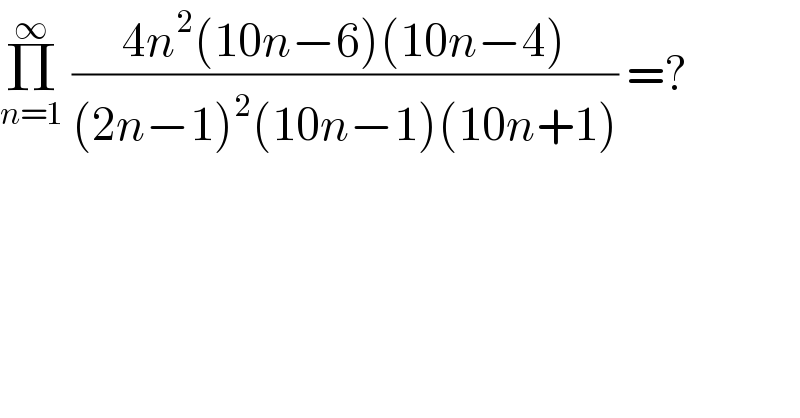
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\:\frac{\mathrm{4}{n}^{\mathrm{2}} \left(\mathrm{10}{n}−\mathrm{6}\right)\left(\mathrm{10}{n}−\mathrm{4}\right)}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{10}{n}−\mathrm{1}\right)\left(\mathrm{10}{n}+\mathrm{1}\right)}\:=? \\ $$
Answered by Olaf last updated on 21/Sep/20
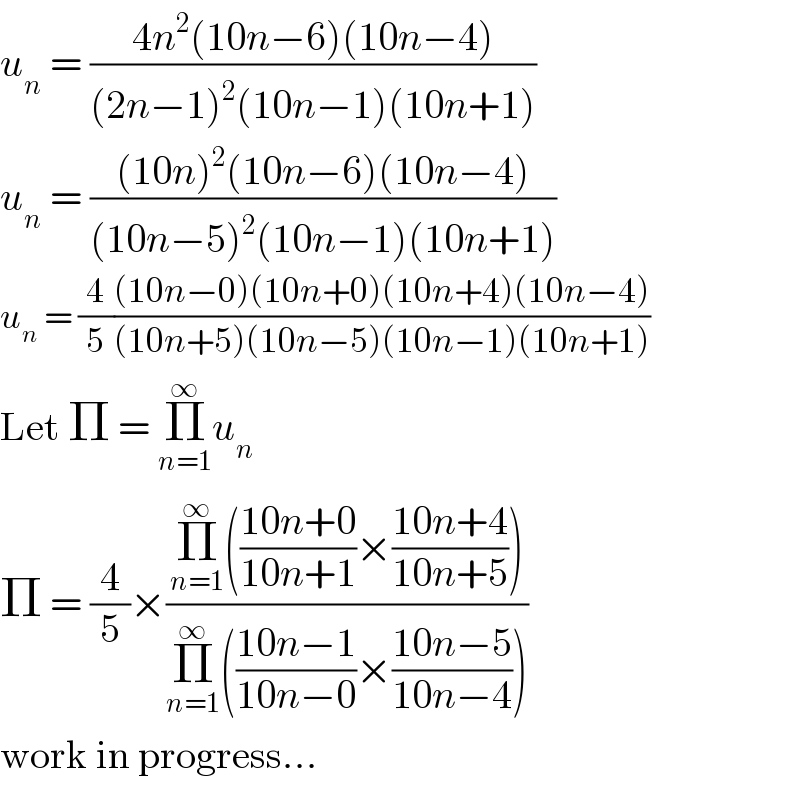
$${u}_{{n}} \:=\:\frac{\mathrm{4}{n}^{\mathrm{2}} \left(\mathrm{10}{n}−\mathrm{6}\right)\left(\mathrm{10}{n}−\mathrm{4}\right)}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{10}{n}−\mathrm{1}\right)\left(\mathrm{10}{n}+\mathrm{1}\right)} \\ $$$${u}_{{n}} \:=\:\frac{\left(\mathrm{10}{n}\right)^{\mathrm{2}} \left(\mathrm{10}{n}−\mathrm{6}\right)\left(\mathrm{10}{n}−\mathrm{4}\right)}{\left(\mathrm{10}{n}−\mathrm{5}\right)^{\mathrm{2}} \left(\mathrm{10}{n}−\mathrm{1}\right)\left(\mathrm{10}{n}+\mathrm{1}\right)} \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{4}}{\mathrm{5}}\frac{\left(\mathrm{10}{n}−\mathrm{0}\right)\left(\mathrm{10}{n}+\mathrm{0}\right)\left(\mathrm{10}{n}+\mathrm{4}\right)\left(\mathrm{10}{n}−\mathrm{4}\right)}{\left(\mathrm{10}{n}+\mathrm{5}\right)\left(\mathrm{10}{n}−\mathrm{5}\right)\left(\mathrm{10}{n}−\mathrm{1}\right)\left(\mathrm{10}{n}+\mathrm{1}\right)} \\ $$$$\mathrm{Let}\:\Pi\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}{u}_{{n}} \\ $$$$\Pi\:=\:\frac{\mathrm{4}}{\mathrm{5}}×\frac{\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\frac{\mathrm{10}{n}+\mathrm{0}}{\mathrm{10}{n}+\mathrm{1}}×\frac{\mathrm{10}{n}+\mathrm{4}}{\mathrm{10}{n}+\mathrm{5}}\right)}{\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\frac{\mathrm{10}{n}−\mathrm{1}}{\mathrm{10}{n}−\mathrm{0}}×\frac{\mathrm{10}{n}−\mathrm{5}}{\mathrm{10}{n}−\mathrm{4}}\right)} \\ $$$$\mathrm{work}\:\mathrm{in}\:\mathrm{progress}… \\ $$
