Question Number 116056 by Study last updated on 30/Sep/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{5}^{{n}} }{{n}!}=? \\ $$
Answered by Dwaipayan Shikari last updated on 30/Sep/20

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}!}=\mathrm{e}^{\mathrm{x}} −\mathrm{1} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{5}^{\mathrm{n}} }{\mathrm{n}!}=\mathrm{e}^{\mathrm{5}} −\mathrm{1} \\ $$
Answered by MWSuSon last updated on 30/Sep/20
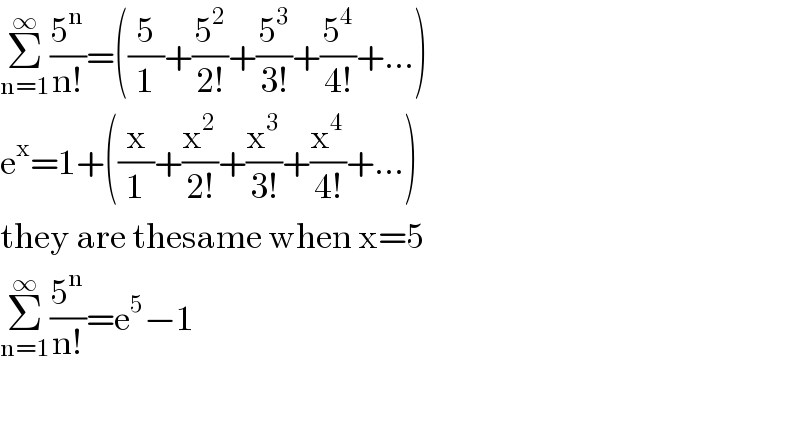
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{5}^{\mathrm{n}} }{\mathrm{n}!}=\left(\frac{\mathrm{5}}{\mathrm{1}}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{5}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{5}^{\mathrm{4}} }{\mathrm{4}!}+…\right) \\ $$$$\mathrm{e}^{\mathrm{x}} =\mathrm{1}+\left(\frac{\mathrm{x}}{\mathrm{1}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}+…\right) \\ $$$$\mathrm{they}\:\mathrm{are}\:\mathrm{thesame}\:\mathrm{when}\:\mathrm{x}=\mathrm{5} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{5}^{\mathrm{n}} }{\mathrm{n}!}=\mathrm{e}^{\mathrm{5}} −\mathrm{1} \\ $$$$ \\ $$
