Question Number 125256 by 676597498 last updated on 09/Dec/20
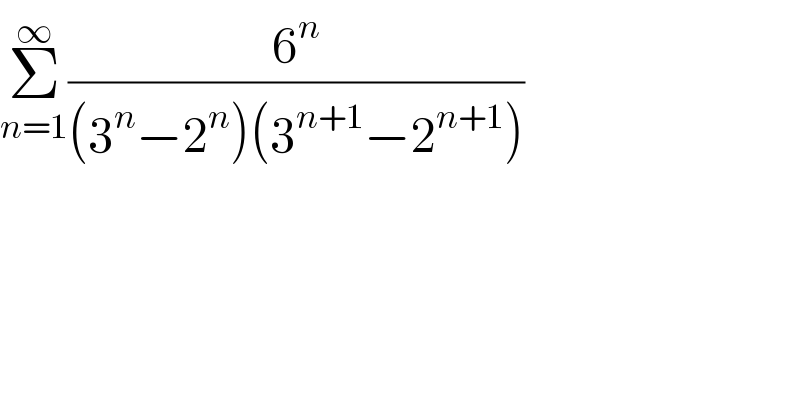
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{6}^{{n}} }{\left(\mathrm{3}^{{n}} −\mathrm{2}^{{n}} \right)\left(\mathrm{3}^{{n}+\mathrm{1}} −\mathrm{2}^{{n}+\mathrm{1}} \right)} \\ $$
Answered by mathmax by abdo last updated on 09/Dec/20

$$\mathrm{let}\:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{6}^{\mathrm{n}} }{\left(\mathrm{3}^{\mathrm{n}} −\mathrm{2}^{\mathrm{n}} \right)\left(\mathrm{3}^{\mathrm{n}+\mathrm{1}} −\mathrm{2}^{\mathrm{n}+\mathrm{1}} \right)}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{3}^{\mathrm{n}} .\mathrm{2}^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}} \left(\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}} \right)\mathrm{3}^{\mathrm{n}+\mathrm{1}} \left(\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}+\mathrm{1}} \right)} \\ $$$$=\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}+\mathrm{1}} \left(\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}} \right)\left(\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}+\mathrm{1}} \right)}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}} }{\left(\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}} \right)\left(\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}+\mathrm{1}} \right)} \\ $$$$\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}\right)}\:=\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}}\right)\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}} }−\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}+\mathrm{1}} }\right)=\mathrm{3}\left(\mathrm{v}_{\mathrm{n}} −\mathrm{v}_{\mathrm{n}+\mathrm{1}} \right)\:\mathrm{with}\:\mathrm{v}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{u}_{\mathrm{k}} =\mathrm{3}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \mathrm{v}_{\mathrm{k}} −\mathrm{v}_{\mathrm{k}+\mathrm{1}} =\mathrm{3}\left\{\mathrm{v}_{\mathrm{1}} −\mathrm{v}_{\mathrm{2}} +\mathrm{v}_{\mathrm{2}} −\mathrm{v}_{\mathrm{3}} +…+\mathrm{v}_{\mathrm{n}} −\mathrm{v}_{\mathrm{n}+\mathrm{1}} \right\} \\ $$$$=\mathrm{3}\left(\mathrm{v}_{\mathrm{1}} −\mathrm{v}_{\mathrm{n}+\mathrm{1}} \right)\:=\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{n}+\mathrm{1}} }\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{u}_{\mathrm{k}} =\mathrm{3}\left(\mathrm{3}−\mathrm{1}\right)\:=\mathrm{6} \\ $$
