n-1-8-n-2-n-

Question Number 148203 by liberty last updated on 26/Jul/21

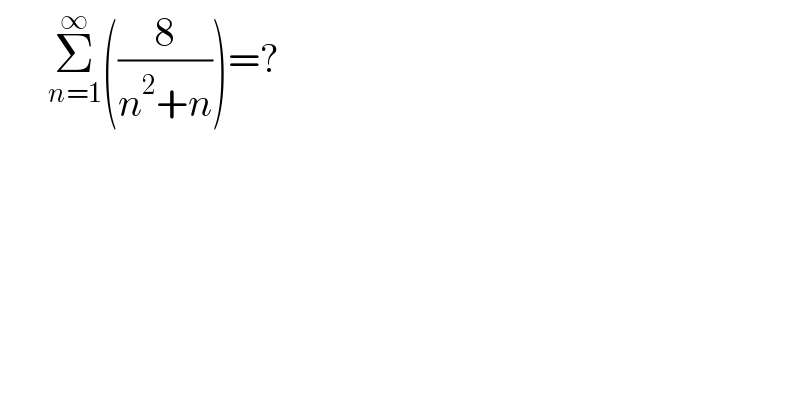
$$\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{8}}{{n}^{\mathrm{2}} +{n}}\right)=? \\ $$

Answered by mathmax by abdo last updated on 26/Jul/21

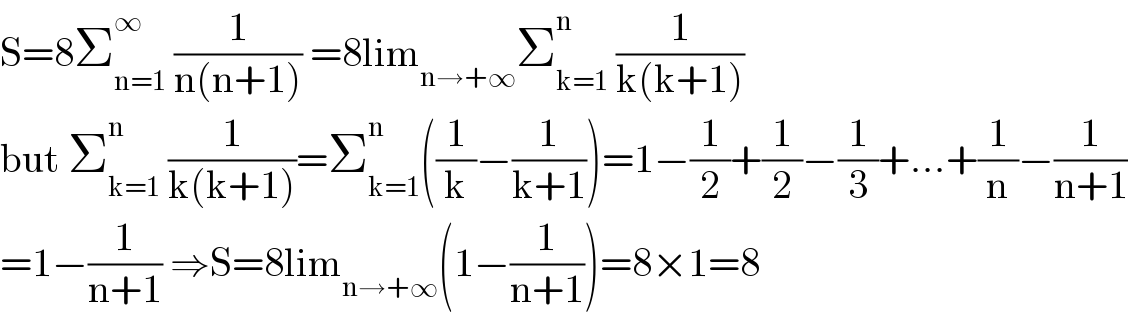
S=8Σ_(n=1) ^∞ (1/(n(n+1))) =8lim_(n→+∞) Σ_(k=1) ^n (1/(k(k+1))) but Σ_(k=1) ^n (1/(k(k+1)))=Σ_(k=1) ^n ((1/k)−(1/(k+1)))=1−(1/2)+(1/2)−(1/3)+...+(1/n)−(1/(n+1)) =1−(1/(n+1)) ⇒S=8lim_(n→+∞) (1−(1/(n+1)))=8×1=8

$$\mathrm{S}=\mathrm{8}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}\:=\mathrm{8lim}_{\mathrm{n}\rightarrow+\infty} \sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)} \\ $$$$\mathrm{but}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\Rightarrow\mathrm{S}=\mathrm{8lim}_{\mathrm{n}\rightarrow+\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)=\mathrm{8}×\mathrm{1}=\mathrm{8} \\ $$

Answered by puissant last updated on 26/Jul/21

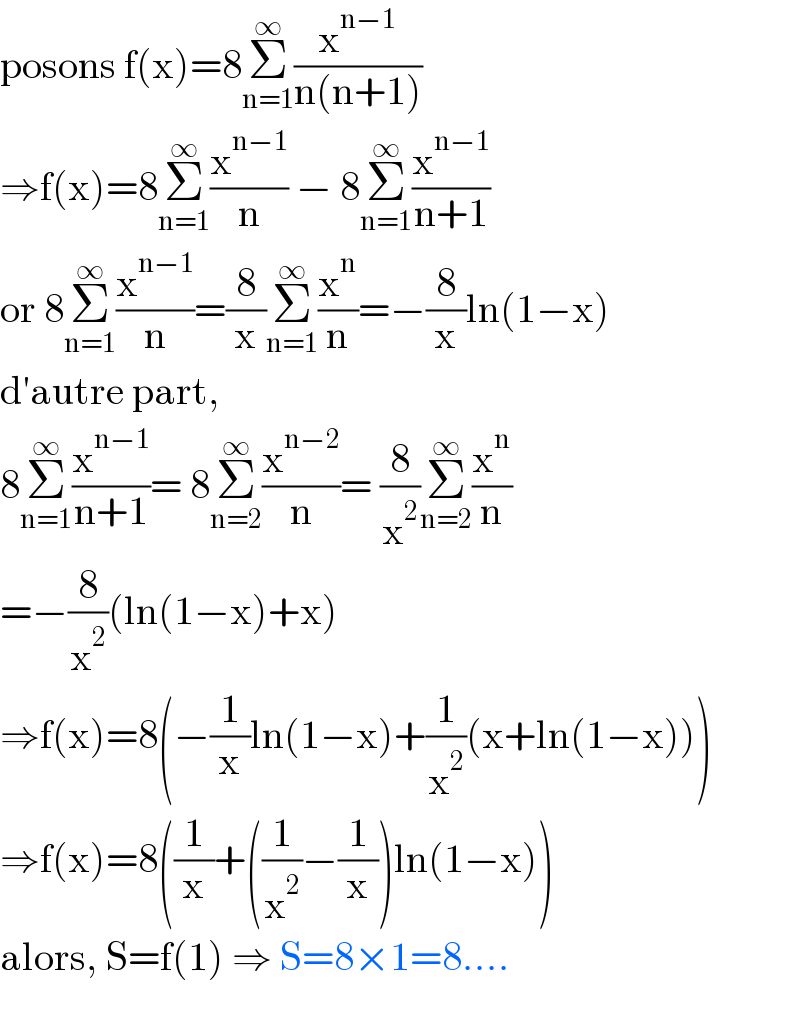
posons f(x)=8Σ_(n=1) ^∞ (x^(n−1) /(n(n+1))) ⇒f(x)=8Σ_(n=1) ^∞ (x^(n−1) /n) − 8Σ_(n=1) ^∞ (x^(n−1) /(n+1)) or 8Σ_(n=1) ^∞ (x^(n−1) /n)=(8/x)Σ_(n=1) ^∞ (x^n /n)=−(8/x)ln(1−x) d′autre part, 8Σ_(n=1) ^∞ (x^(n−1) /(n+1))= 8Σ_(n=2) ^∞ (x^(n−2) /n)= (8/x^2 )Σ_(n=2) ^∞ (x^n /n) =−(8/x^2 )(ln(1−x)+x) ⇒f(x)=8(−(1/x)ln(1−x)+(1/x^2 )(x+ln(1−x))) ⇒f(x)=8((1/x)+((1/x^2 )−(1/x))ln(1−x)) alors, S=f(1) ⇒ S=8×1=8....

$$\mathrm{posons}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{8}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{8}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:−\:\mathrm{8}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{or}\:\mathrm{8}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}=\frac{\mathrm{8}}{\mathrm{x}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}=−\frac{\mathrm{8}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right) \\ $$$$\mathrm{d}'\mathrm{autre}\:\mathrm{part},\: \\ $$$$\mathrm{8}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}+\mathrm{1}}=\:\mathrm{8}\underset{\mathrm{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{2}} }{\mathrm{n}}=\:\frac{\mathrm{8}}{\mathrm{x}^{\mathrm{2}} }\underset{\mathrm{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}} \\ $$$$=−\frac{\mathrm{8}}{\mathrm{x}^{\mathrm{2}} }\left(\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)+\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{8}\left(−\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\left(\mathrm{x}+\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right)\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{8}\left(\frac{\mathrm{1}}{\mathrm{x}}+\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right) \\ $$$$\mathrm{alors},\:\mathrm{S}=\mathrm{f}\left(\mathrm{1}\right)\:\Rightarrow\:\mathrm{S}=\mathrm{8}×\mathrm{1}=\mathrm{8}…. \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply