Menu Close

n-1-m-1-1-m-2-n-mn-2-2mn-

Tinku Tara 0 Comments
Pin




Question Number 166160 by cortano1 last updated on 14/Feb/22
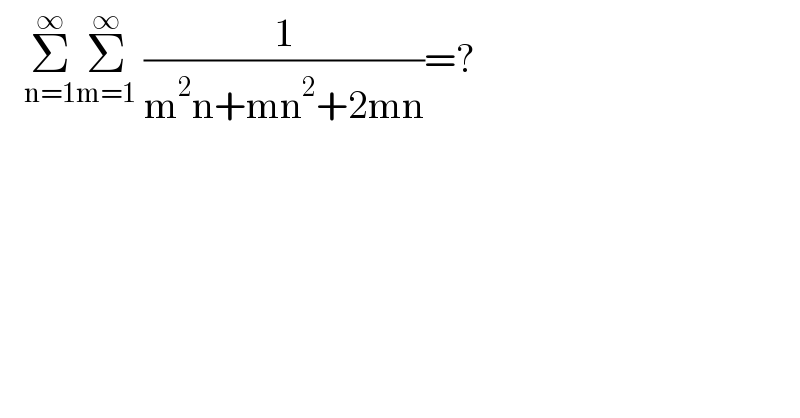
Σ_(n=1) ^∞ Σ_(m=1) ^∞ (1/(m^2 n+mn^2 +2mn))=?
$$\:\:\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{m}^{\mathrm{2}} \mathrm{n}+\mathrm{mn}^{\mathrm{2}} +\mathrm{2mn}}=? \\ $$
Answered by Jamshidbek last updated on 14/Feb/22
Commented by amin96 last updated on 14/Feb/22
bravooo sir
$$\boldsymbol{\mathrm{bravooo}}\:\boldsymbol{\mathrm{sir}} \\ $$
Answered by cortano1 last updated on 14/Feb/22
S=Σ_(n=1) ^∞ Σ_(m=1) ^∞ (1/n).(1/(m(m+n+2))) = Σ_(n=1) ^∞ Σ_(m=1) ^∞ (1/(n(n+2))).((1/m)−(1/(m+n+2))) = Σ_(n=1) ^∞ (1/(n(n+2)))(1+(1/2)+(1/3)+...+(1/(n+2))) = Σ_(n=1) ^∞ (1/2)((1/n)−(1/(n+2)))(1+(1/2)+(1/3)+...+(1/(n+2))) = (1/2) [ Σ_(n=1) ^∞ (1/n)(1+(1/2)+(1/3)+...+(1/(n+2)))−Σ_(n=3) ^∞ (1/n)(1+(1/2)+...+(1/n)) =(1/2)[ ((23)/8)+Σ_(n=3) ^∞ (1/n)((1/(n+1))+(1/(n+2))) = ((23)/(16))+(1/2)Σ_(n=3) ^∞ ((1/(n(n+1)))+(1/(n(n+2)))) =((23)/(16))+(1/2)[ Σ_(n=3) ^∞ ((1/n)−(1/(n+1))) +Σ_(n=3) ^∞ (1/2)((1/n)−(1/(n+2)))] =((23)/(16))+(1/2)[(1/3)+(1/2)((1/3)+(1/4))]=(7/4)
$$\:\mathrm{S}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}}.\frac{\mathrm{1}}{\mathrm{m}\left(\mathrm{m}+\mathrm{n}+\mathrm{2}\right)} \\ $$$$\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{2}\right)}.\left(\frac{\mathrm{1}}{\mathrm{m}}−\frac{\mathrm{1}}{\mathrm{m}+\mathrm{n}+\mathrm{2}}\right) \\ $$$$\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{2}\right)}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right) \\ $$$$\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right) \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)−\underset{\mathrm{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+…+\frac{\mathrm{1}}{\mathrm{n}}\right)\right. \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{23}}{\mathrm{8}}+\underset{\mathrm{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)\right. \\ $$$$\:=\:\frac{\mathrm{23}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{3}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{2}\right)}\right) \\ $$$$\:=\frac{\mathrm{23}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}\left[\:\underset{\mathrm{n}=\mathrm{3}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)\:+\underset{\mathrm{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)\right] \\ $$$$\:=\frac{\mathrm{23}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\right]=\frac{\mathrm{7}}{\mathrm{4}} \\ $$
Answered by qaz last updated on 14/Feb/22
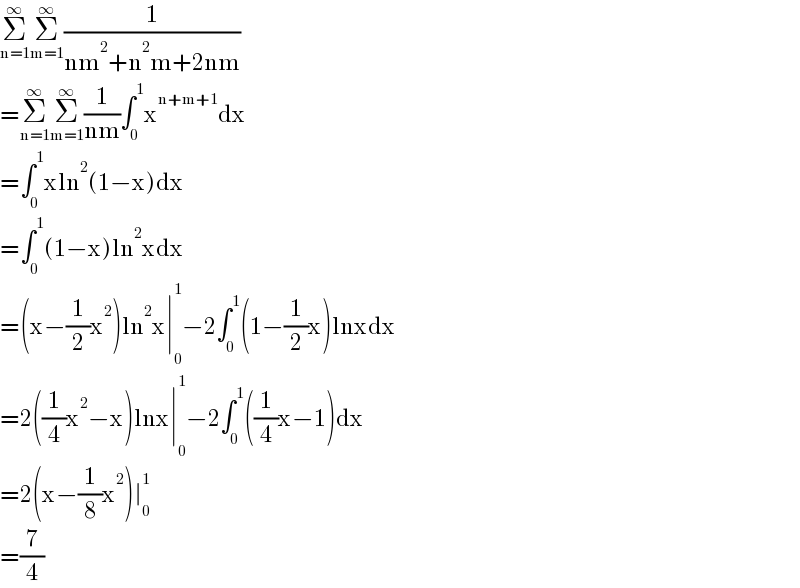
Σ_(n=1) ^∞ Σ_(m=1) ^∞ (1/(nm^2 +n^2 m+2nm)) =Σ_(n=1) ^∞ Σ_(m=1) ^∞ (1/(nm))∫_0 ^1 x^(n+m+1) dx =∫_0 ^1 xln^2 (1−x)dx =∫_0 ^1 (1−x)ln^2 xdx =(x−(1/2)x^2 )ln^2 x∣_0 ^1 −2∫_0 ^1 (1−(1/2)x)lnxdx =2((1/4)x^2 −x)lnx∣_0 ^1 −2∫_0 ^1 ((1/4)x−1)dx =2(x−(1/8)x^2 )∣_0 ^1 =(7/4)
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{nm}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \mathrm{m}+\mathrm{2nm}} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{m}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{nm}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}+\mathrm{m}+\mathrm{1}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xln}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{xdx} \\ $$$$=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)\mathrm{ln}^{\mathrm{2}} \mathrm{x}\mid_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)\mathrm{lnxdx} \\ $$$$=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)\mathrm{lnx}\mid_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$=\mathrm{2}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{7}}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *