Menu Close

n-1-n-2n-1-help-me-pls-

Tinku Tara 0 Comments
Pin




Question Number 100468 by Mikael_786 last updated on 26/Jun/20
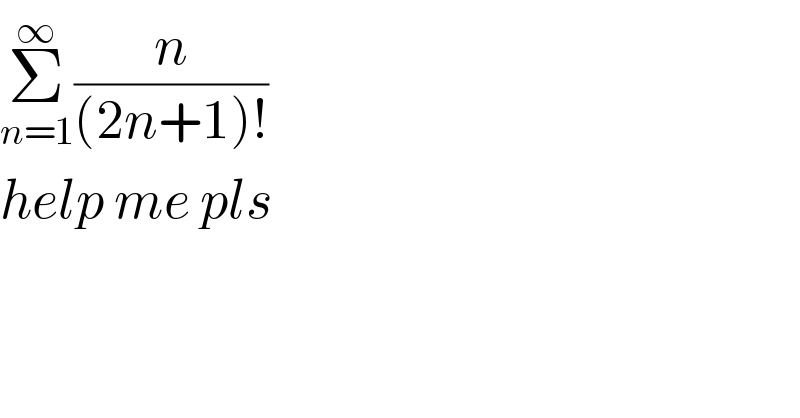
Σ_(n=1) ^∞ (n/((2n+1)!)) help me pls
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$${help}\:{me}\:{pls} \\ $$
Answered by mathmax by abdo last updated on 26/Jun/20
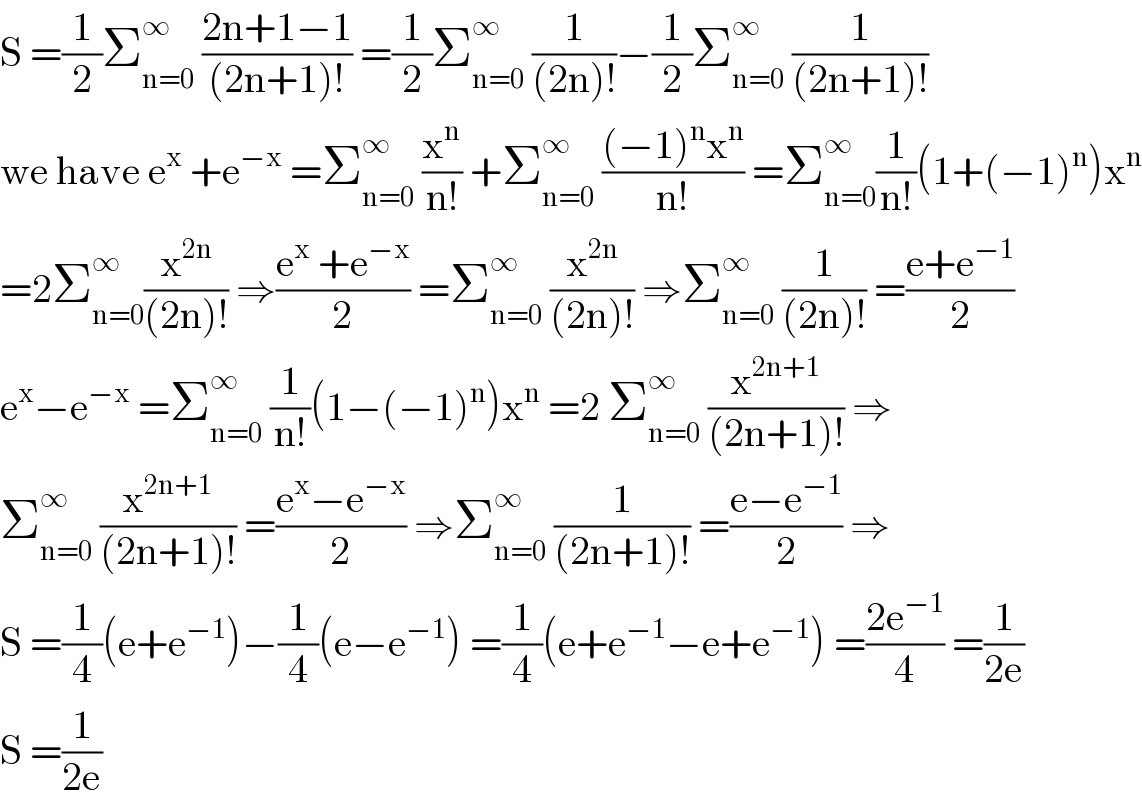
S =(1/2)Σ_(n=0) ^∞ ((2n+1−1)/((2n+1)!)) =(1/2)Σ_(n=0) ^∞ (1/((2n)!))−(1/2)Σ_(n=0) ^∞ (1/((2n+1)!)) we have e^x +e^(−x) =Σ_(n=0) ^∞ (x^n /(n!)) +Σ_(n=0) ^∞ (((−1)^n x^n )/(n!)) =Σ_(n=0) ^∞ (1/(n!))(1+(−1)^n )x^n =2Σ_(n=0) ^∞ (x^(2n) /((2n)!)) ⇒((e^x +e^(−x) )/2) =Σ_(n=0) ^∞ (x^(2n) /((2n)!)) ⇒Σ_(n=0) ^∞ (1/((2n)!)) =((e+e^(−1) )/2) e^x −e^(−x) =Σ_(n=0) ^∞ (1/(n!))(1−(−1)^n )x^n =2 Σ_(n=0) ^∞ (x^(2n+1) /((2n+1)!)) ⇒ Σ_(n=0) ^∞ (x^(2n+1) /((2n+1)!)) =((e^x −e^(−x) )/2) ⇒Σ_(n=0) ^∞ (1/((2n+1)!)) =((e−e^(−1) )/2) ⇒ S =(1/4)(e+e^(−1) )−(1/4)(e−e^(−1) ) =(1/4)(e+e^(−1) −e+e^(−1) ) =((2e^(−1) )/4) =(1/(2e)) S =(1/(2e))
$$\mathrm{S}\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2n}+\mathrm{1}−\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)!}\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}\right)!}−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)!} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{−\mathrm{x}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}!}\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}} }{\mathrm{n}!}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{n}!}\left(\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{n}} \right)\mathrm{x}^{\mathrm{n}} \\ $$$$=\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}\:\Rightarrow\frac{\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}\right)!}\:=\frac{\mathrm{e}+\mathrm{e}^{−\mathrm{1}} }{\mathrm{2}} \\ $$$$\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}!}\left(\mathrm{1}−\left(−\mathrm{1}\right)^{\mathrm{n}} \right)\mathrm{x}^{\mathrm{n}} \:=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:=\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)!}\:=\frac{\mathrm{e}−\mathrm{e}^{−\mathrm{1}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{S}\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{e}+\mathrm{e}^{−\mathrm{1}} \right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{e}−\mathrm{e}^{−\mathrm{1}} \right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{e}+\mathrm{e}^{−\mathrm{1}} −\mathrm{e}+\mathrm{e}^{−\mathrm{1}} \right)\:=\frac{\mathrm{2e}^{−\mathrm{1}} }{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{2e}} \\ $$$$\mathrm{S}\:=\frac{\mathrm{1}}{\mathrm{2e}} \\ $$
Commented by Mikael_786 last updated on 27/Jun/20
thank you Sir
$${thank}\:{you}\:{Sir} \\ $$
Answered by smridha last updated on 26/Jun/20
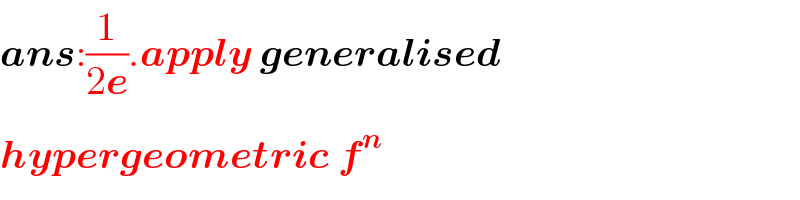
ans:(1/(2e)).apply generalised hypergeometric f^n
$$\boldsymbol{{ans}}:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{e}}}.\boldsymbol{{apply}}\:\boldsymbol{{generalised}} \\ $$$$\boldsymbol{{hypergeometric}}\:\boldsymbol{{f}}^{\boldsymbol{{n}}} \\ $$
Answered by maths mind last updated on 26/Jun/20
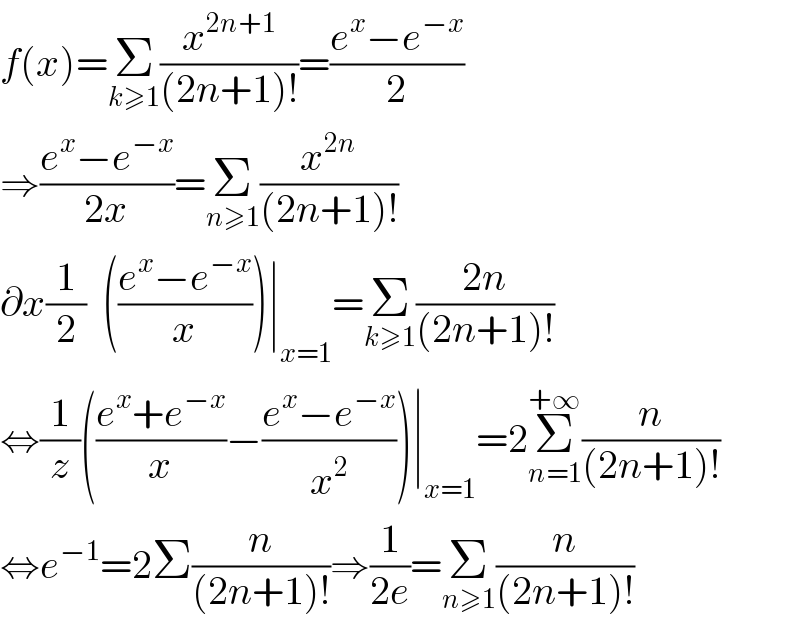
f(x)=Σ_(k≥1) (x^(2n+1) /((2n+1)!))=((e^x −e^(−x) )/2) ⇒((e^x −e^(−x) )/(2x))=Σ_(n≥1) (x^(2n) /((2n+1)!)) ∂x(1/2) (((e^x −e^(−x) )/x))∣_(x=1) =Σ_(k≥1) ((2n)/((2n+1)!)) ⇔(1/z)(((e^x +e^(−x) )/x)−((e^x −e^(−x) )/x^2 ))∣_(x=1) =2Σ_(n=1) ^(+∞) (n/((2n+1)!)) ⇔e^(−1) =2Σ(n/((2n+1)!))⇒(1/(2e))=Σ_(n≥1) (n/((2n+1)!))
$${f}\left({x}\right)=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}} \\ $$$$\Rightarrow\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}{x}}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\partial{x}\frac{\mathrm{1}}{\mathrm{2}}\:\:\left(\frac{{e}^{{x}} −{e}^{−{x}} }{{x}}\right)\mid_{{x}=\mathrm{1}} =\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{2}{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{{z}}\left(\frac{{e}^{{x}} +{e}^{−{x}} }{{x}}−\frac{{e}^{{x}} −{e}^{−{x}} }{{x}^{\mathrm{2}} }\right)\mid_{{x}=\mathrm{1}} =\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\Leftrightarrow{e}^{−\mathrm{1}} =\mathrm{2}\Sigma\frac{{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}{e}}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$
Commented by Mikael_786 last updated on 27/Jun/20
thank you Sir
$${thank}\:{you}\:{Sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *