Question Number 102784 by bobhans last updated on 11/Jul/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}}{\mathrm{4}^{{n}} }\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 11/Jul/20
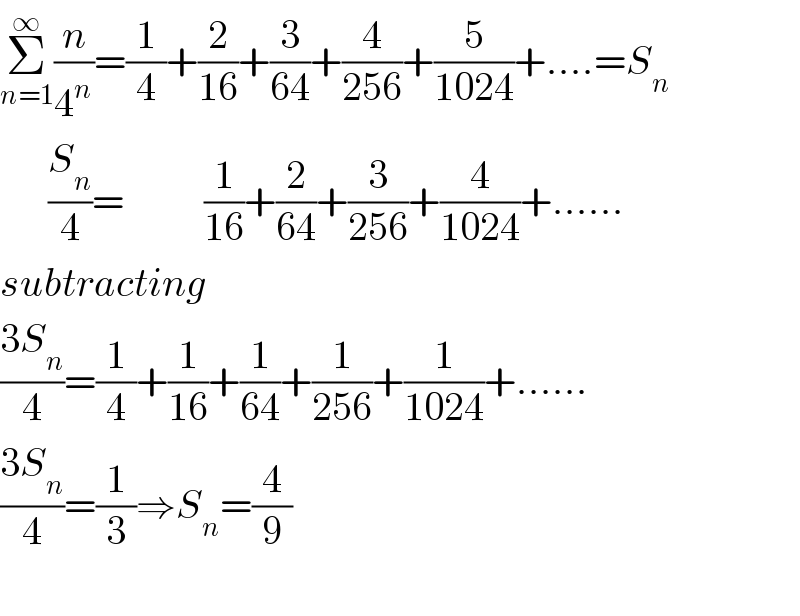
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\mathrm{4}^{{n}} }=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{2}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{64}}+\frac{\mathrm{4}}{\mathrm{256}}+\frac{\mathrm{5}}{\mathrm{1024}}+….={S}_{{n}} \\ $$$$\:\:\:\:\:\:\frac{{S}_{{n}} }{\mathrm{4}}=\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{2}}{\mathrm{64}}+\frac{\mathrm{3}}{\mathrm{256}}+\frac{\mathrm{4}}{\mathrm{1024}}+…… \\ $$$${subtracting} \\ $$$$\frac{\mathrm{3}{S}_{{n}} }{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{64}}+\frac{\mathrm{1}}{\mathrm{256}}+\frac{\mathrm{1}}{\mathrm{1024}}+…… \\ $$$$\frac{\mathrm{3}{S}_{{n}} }{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{S}_{{n}} =\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$ \\ $$
Answered by bramlex last updated on 11/Jul/20

$$\mathrm{let}\:\mathrm{S}\:=\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{n}+\mathrm{1}}{\mathrm{4}^{\mathrm{n}} }\:\&\:\mathrm{X}=\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{n}}{\mathrm{4}^{\mathrm{n}} } \\ $$$$\Leftrightarrow\mathrm{S}\:=\:\mathrm{X}+\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{n}} }\: \\ $$$$\mathrm{S}\:=\:\mathrm{X}\:+\:\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}\:;\left(\mathrm{geometric}\:\mathrm{P}\:\right) \\ $$$$\mathrm{S}\:=\:\mathrm{X}+\frac{\mathrm{1}}{\mathrm{3}}\:.\:\mathrm{in}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hand}\: \\ $$$$\mathrm{we}\:\mathrm{have}\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}+\mathrm{1}}{\mathrm{4}^{\mathrm{n}} }\:=\:\mathrm{4}\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}}{\mathrm{4}^{\mathrm{n}} }\:−\mathrm{1} \\ $$$$\mathrm{S}\:=\:\mathrm{4X}−\mathrm{1}\:=\:\mathrm{X}+\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow\mathrm{3X}=\frac{\mathrm{4}}{\mathrm{3}};\:\mathrm{X}\:=\:\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\underset{\mathrm{n}\:=\:\mathrm{1}\:} {\overset{\infty} {\sum}}\:\frac{\mathrm{n}}{\mathrm{4}^{\mathrm{n}} }\:=\:\frac{\mathrm{4}}{\mathrm{9}}\:\bullet\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 11/Jul/20
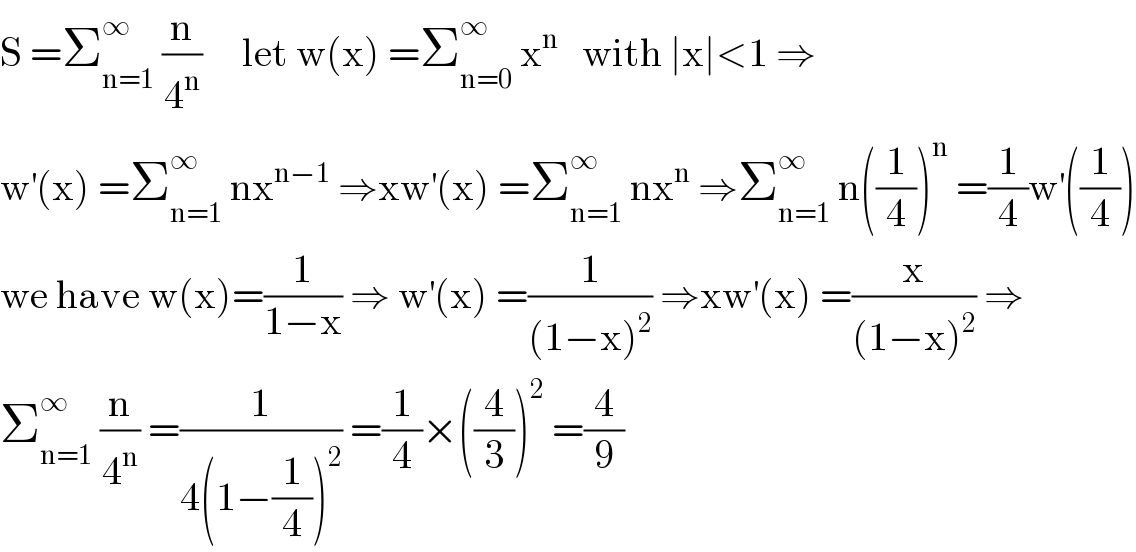
$$\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}}{\mathrm{4}^{\mathrm{n}} }\:\:\:\:\:\mathrm{let}\:\mathrm{w}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\:\:\mathrm{with}\:\mid\mathrm{x}\mid<\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{w}^{'} \left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\mathrm{xw}^{'} \left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{w}^{'} \left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{w}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\:\mathrm{w}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{xw}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}}{\mathrm{4}^{\mathrm{n}} }\:=\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}×\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} \:=\frac{\mathrm{4}}{\mathrm{9}} \\ $$
