Menu Close

n-1-n-n-1-n-2-n-3-

Tinku Tara 0 Comments
Pin




Question Number 105571 by bobhans last updated on 30/Jul/20
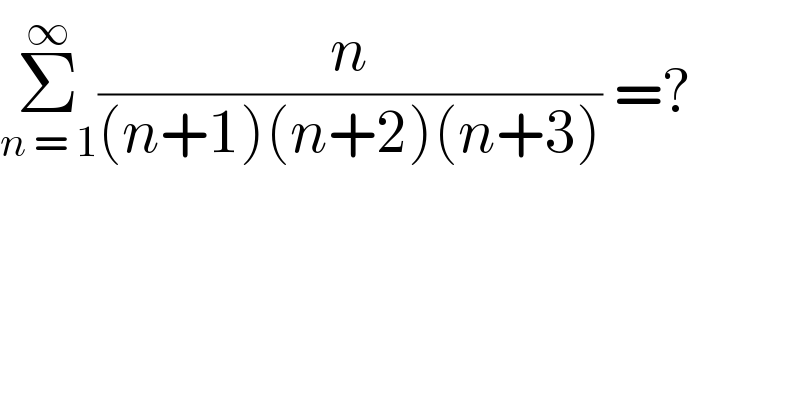
Σ_(n = 1) ^∞ (n/((n+1)(n+2)(n+3))) =?
$$\underset{{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}\:=? \\ $$
Answered by bubugne last updated on 30/Jul/20
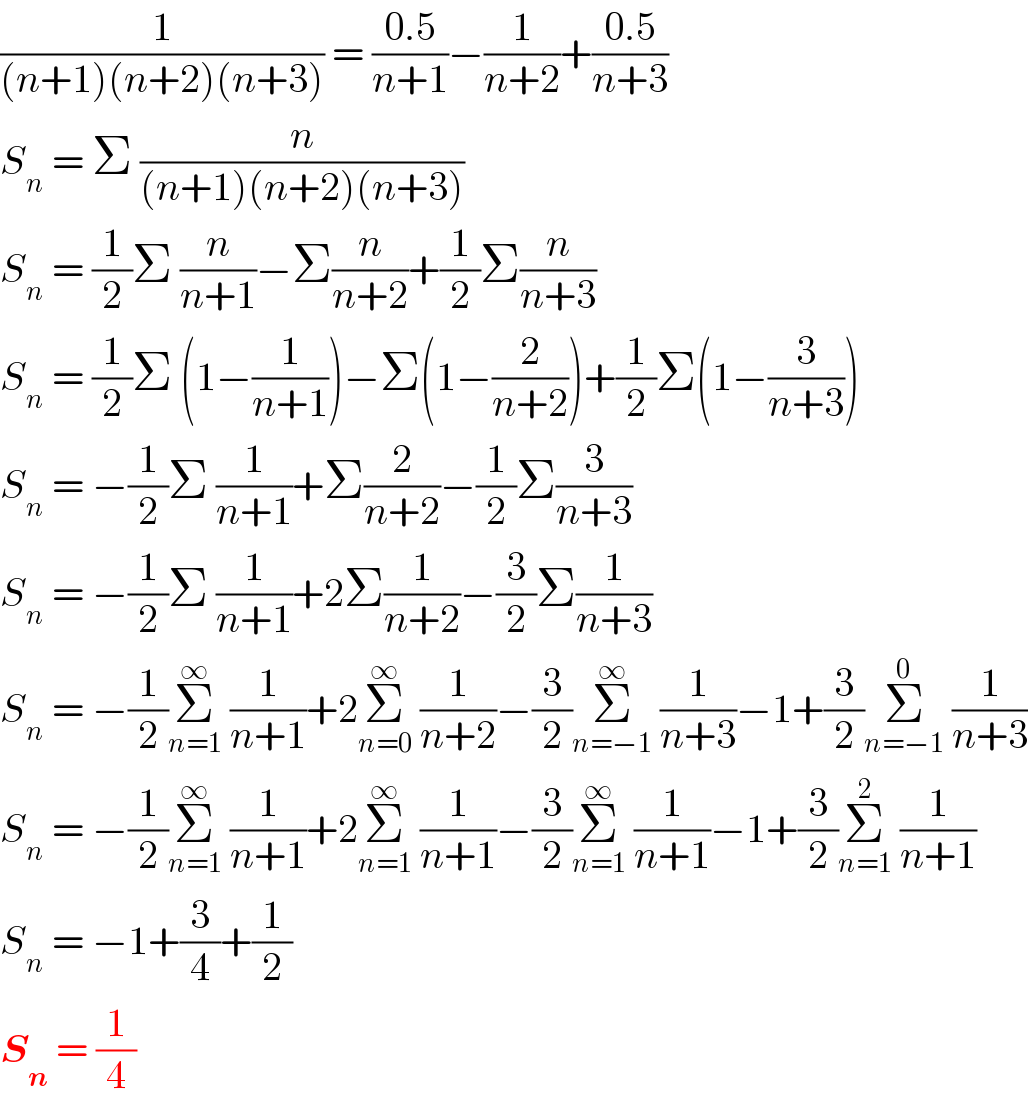
(1/((n+1)(n+2)(n+3))) = ((0.5)/(n+1))−(1/(n+2))+((0.5)/(n+3)) S_n = Σ (n/((n+1)(n+2)(n+3))) S_n = (1/2)Σ (n/(n+1))−Σ(n/(n+2))+(1/2)Σ(n/(n+3)) S_n = (1/2)Σ (1−(1/(n+1)))−Σ(1−(2/(n+2)))+(1/2)Σ(1−(3/(n+3))) S_n = −(1/2)Σ (1/(n+1))+Σ(2/(n+2))−(1/2)Σ(3/(n+3)) S_n = −(1/2)Σ (1/(n+1))+2Σ(1/(n+2))−(3/2)Σ(1/(n+3)) S_n = −(1/2)Σ_(n=1) ^∞ (1/(n+1))+2Σ_(n=0) ^∞ (1/(n+2))−(3/2)Σ_(n=−1) ^∞ (1/(n+3))−1+(3/2)Σ_(n=−1) ^0 (1/(n+3)) S_n = −(1/2)Σ_(n=1) ^∞ (1/(n+1))+2Σ_(n=1) ^∞ (1/(n+1))−(3/2)Σ_(n=1) ^∞ (1/(n+1))−1+(3/2)Σ_(n=1) ^2 (1/(n+1)) S_n = −1+(3/4)+(1/2) S_n = (1/4)
$$\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}\:=\:\frac{\mathrm{0}.\mathrm{5}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}+\frac{\mathrm{0}.\mathrm{5}}{{n}+\mathrm{3}} \\ $$$${S}_{{n}} \:=\:\Sigma\:\frac{{n}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}\: \\ $$$${S}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\Sigma\:\frac{{n}}{{n}+\mathrm{1}}−\Sigma\frac{{n}}{{n}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{{n}}{{n}+\mathrm{3}} \\ $$$${S}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\Sigma\:\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)−\Sigma\left(\mathrm{1}−\frac{\mathrm{2}}{{n}+\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left(\mathrm{1}−\frac{\mathrm{3}}{{n}+\mathrm{3}}\right) \\ $$$${S}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}\Sigma\:\frac{\mathrm{1}}{{n}+\mathrm{1}}+\Sigma\frac{\mathrm{2}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{\mathrm{3}}{{n}+\mathrm{3}} \\ $$$${S}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}\Sigma\:\frac{\mathrm{1}}{{n}+\mathrm{1}}+\mathrm{2}\Sigma\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\Sigma\frac{\mathrm{1}}{{n}+\mathrm{3}} \\ $$$${S}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}+\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\underset{{n}=−\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{3}}−\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\underset{{n}=−\mathrm{1}} {\overset{\mathrm{0}} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{3}} \\ $$$${S}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}−\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$${S}_{{n}} \:=\:−\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{{S}}_{\boldsymbol{{n}}} \:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by bobhans last updated on 30/Jul/20
jooss and cooll
$${jooss}\:{and}\:{cooll} \\ $$
Answered by Ar Brandon last updated on 30/Jul/20
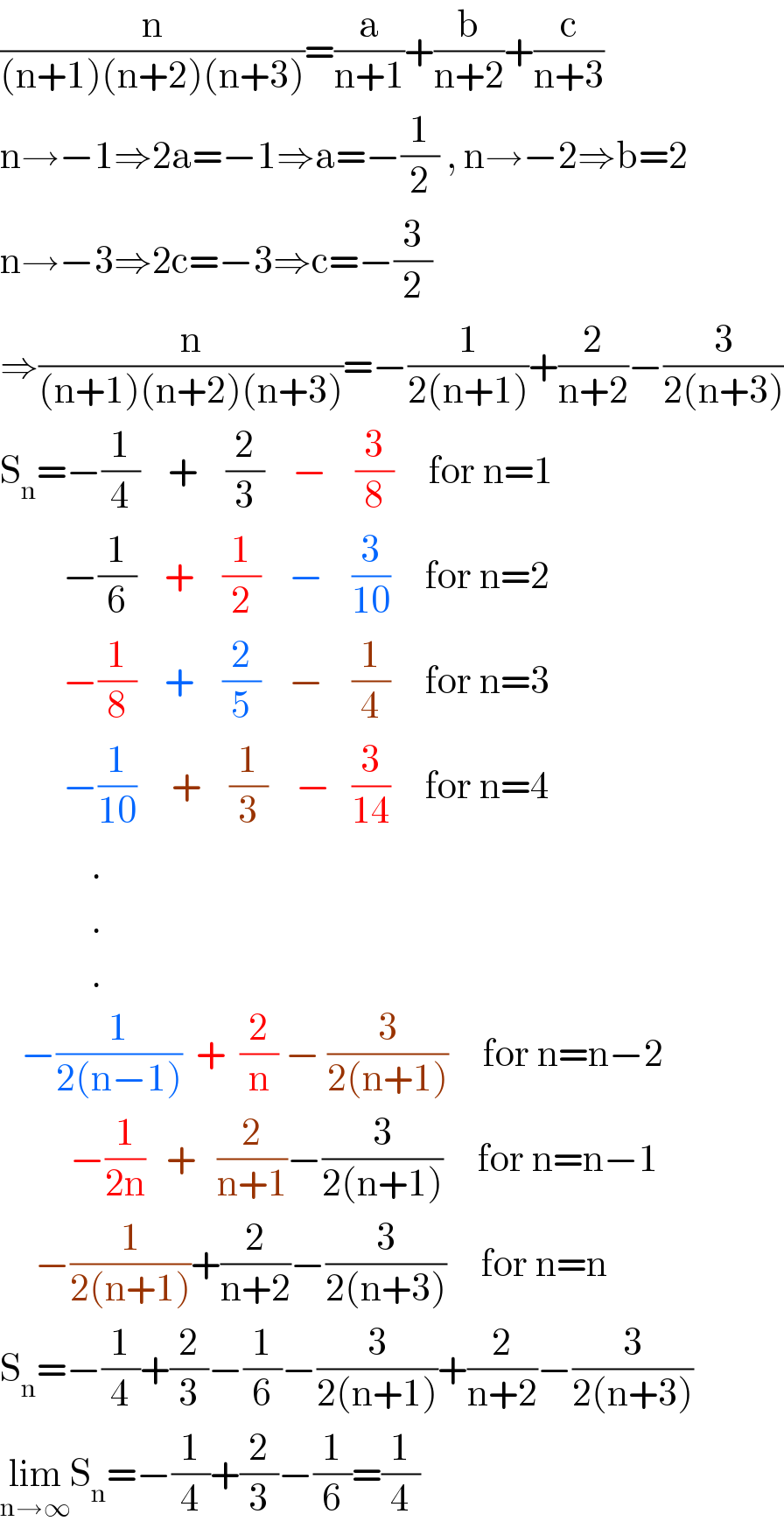
(n/((n+1)(n+2)(n+3)))=(a/(n+1))+(b/(n+2))+(c/(n+3)) n→−1⇒2a=−1⇒a=−(1/2) , n→−2⇒b=2 n→−3⇒2c=−3⇒c=−(3/2) ⇒(n/((n+1)(n+2)(n+3)))=−(1/(2(n+1)))+(2/(n+2))−(3/(2(n+3))) S_n =−(1/4) + (2/3) − (3/8) for n=1 −(1/6) + (1/2) − (3/(10)) for n=2 −(1/8) + (2/5) − (1/4) for n=3 −(1/(10)) + (1/3) − (3/(14)) for n=4 . . . −(1/(2(n−1))) + (2/n) − (3/(2(n+1))) for n=n−2 −(1/(2n)) + (2/(n+1))−(3/(2(n+1))) for n=n−1 −(1/(2(n+1)))+(2/(n+2))−(3/(2(n+3))) for n=n S_n =−(1/4)+(2/3)−(1/6)−(3/(2(n+1)))+(2/(n+2))−(3/(2(n+3))) lim_(n→∞) S_n =−(1/4)+(2/3)−(1/6)=(1/4)
$$\frac{\mathrm{n}}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{3}\right)}=\frac{\mathrm{a}}{\mathrm{n}+\mathrm{1}}+\frac{\mathrm{b}}{\mathrm{n}+\mathrm{2}}+\frac{\mathrm{c}}{\mathrm{n}+\mathrm{3}} \\ $$$$\mathrm{n}\rightarrow−\mathrm{1}\Rightarrow\mathrm{2a}=−\mathrm{1}\Rightarrow\mathrm{a}=−\frac{\mathrm{1}}{\mathrm{2}}\:,\:\mathrm{n}\rightarrow−\mathrm{2}\Rightarrow\mathrm{b}=\mathrm{2} \\ $$$$\mathrm{n}\rightarrow−\mathrm{3}\Rightarrow\mathrm{2c}=−\mathrm{3}\Rightarrow\mathrm{c}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{n}}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{3}\right)}=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{n}+\mathrm{3}\right)} \\ $$$$\mathrm{S}_{\mathrm{n}} =−\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:+\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:−\:\:\:\:\frac{\mathrm{3}}{\mathrm{8}}\:\:\:\:\:\mathrm{for}\:\mathrm{n}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\:+\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:−\:\:\:\:\frac{\mathrm{3}}{\mathrm{10}}\:\:\:\:\:\mathrm{for}\:\mathrm{n}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{8}}\:\:\:\:+\:\:\:\:\frac{\mathrm{2}}{\mathrm{5}}\:\:\:\:−\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\mathrm{for}\:\mathrm{n}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{10}}\:\:\:\:\:+\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:−\:\:\:\frac{\mathrm{3}}{\mathrm{14}}\:\:\:\:\:\mathrm{for}\:\mathrm{n}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:. \\ $$$$\:\:\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{n}−\mathrm{1}\right)}\:\:+\:\:\frac{\mathrm{2}}{\mathrm{n}}\:−\:\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)}\:\:\:\:\:\mathrm{for}\:\mathrm{n}=\mathrm{n}−\mathrm{2}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2n}}\:\:\:+\:\:\:\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)}\:\:\:\:\:\mathrm{for}\:\mathrm{n}=\mathrm{n}−\mathrm{1} \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{n}+\mathrm{3}\right)}\:\:\:\:\:\mathrm{for}\:\mathrm{n}=\mathrm{n} \\ $$$$\mathrm{S}_{\mathrm{n}} =−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{n}+\mathrm{3}\right)} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}S}_{\mathrm{n}} =−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by nimnim last updated on 30/Jul/20
(n/((n+1)(n+2)(n+3)))=(((n+1)+(n+2)−(n+3))/((n+1)(n+2)(n+3))) =(1/((n+2)(n+3)))+(1/((n+1)(n+3)))−(1/((n+1)(n+2))) =[(1/(n+2))−(1/(n+3))]+(1/2)[(1/(n+1))−(1/(n+3))]−[(1/(n+1))−(1/(n+2))] =Σ_(n=1) ^∞ [(1/(n+2))−(1/(n+3))]+Σ_(n=1) ^∞ (1/2)[(1/(n+1))−(1/(n+3))]−Σ_(n=1) ^∞ [(1/(n+1))−(1/(n+2))] note: all are nth terms of telescoping series =lim_(n→∞) [(1/3)−(1/(n+3))]+(1/2)lim_(n→∞) [(1/2)+(1/3)−(1/(n−2))−(1/(n+3))]−lim_(n→∞) [(1/2)−(1/(n+2))] =[(1/3)−0]+(1/2)[(1/2)+(1/3)−0−0]−[(1/2)−0] =(1/3)+(5/(12))−(1/2)=((4+5−6)/(12))=(3/(12))= (1/4)■
$$\frac{{n}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}=\frac{\left({n}+\mathrm{1}\right)+\left({n}+\mathrm{2}\right)−\left({n}+\mathrm{3}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{3}\right)}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$=\left[\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right]+\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right]−\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right] \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right]+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right]−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right] \\ $$$${note}:\:{all}\:{are}\:{nth}\:{terms}\:{of}\:{telescoping}\:{series} \\ $$$$\:=\underset{{n}\rightarrow\infty} {{lim}}\left[\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right]+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\rightarrow\infty} {{lim}}\left[\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{{n}−\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right]−\underset{{n}\rightarrow\infty} {{lim}}\:\left[\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right] \\ $$$$\:=\left[\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{0}\right]+\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{0}−\mathrm{0}\right]−\left[\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{0}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{5}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{4}+\mathrm{5}−\mathrm{6}}{\mathrm{12}}=\frac{\mathrm{3}}{\mathrm{12}}=\:\frac{\mathrm{1}}{\mathrm{4}}\blacksquare \\ $$
Answered by Dwaipayan Shikari last updated on 30/Jul/20
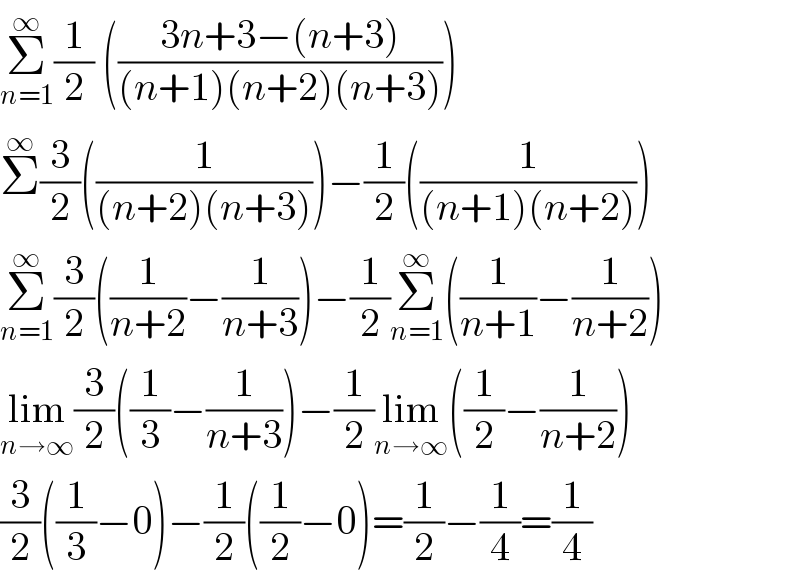
Σ_(n=1) ^∞ (1/2) (((3n+3−(n+3))/((n+1)(n+2)(n+3)))) Σ^∞ (3/2)((1/((n+2)(n+3))))−(1/2)((1/((n+1)(n+2)))) Σ_(n=1) ^∞ (3/2)((1/(n+2))−(1/(n+3)))−(1/2)Σ_(n=1) ^∞ ((1/(n+1))−(1/(n+2))) lim_(n→∞) (3/2)((1/3)−(1/(n+3)))−(1/2)lim_(n→∞) ((1/2)−(1/(n+2))) (3/2)((1/3)−0)−(1/2)((1/2)−0)=(1/2)−(1/4)=(1/4)
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\:\left(\frac{\mathrm{3}{n}+\mathrm{3}−\left({n}+\mathrm{3}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}\right) \\ $$$$\overset{\infty} {\sum}\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{0}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by Ar Brandon last updated on 30/Jul/20
wow ! Better than mine.��

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *